
【题目】如图,在Rt△ABC中,∠BAC=90°,AB>AC,射线AM平分∠BAC.
(1)设AM交BC于点D,DE⊥AB于点E,DF⊥AC于点F,连接EF.有以下三种“判断”:
判断1:AD垂直平分EF.
判断2:EF垂直平分AD.
判断3:AD与EF互相垂直平分.
你同意哪个“判断”?简述理由;
(2)若射线AM上有一点N到△ABC的顶点B,C的距离相等,连接NB,NC.
①请指出△NBC的形状,并说明理由;
②当AB=11,AC=7时,求四边形ABNC的面积.
【答案】
(1)
解:如图,判断3正确.理由如下:
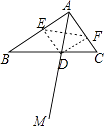
∵∠BAC=90°,DE⊥ABDF⊥AC,
∴DE=DF,∴∠AED=∠AFD=∠EAF=90°,
∴四边形AEDF是矩形,∵DE=DF,
∴四边形AEDF是正方形,
∴AD与EF互相垂直平分.
故判断3正确
(2)
解:①结论:△BCN是等腰直角三角形.理由如下:
如图作NE⊥AB于E,FN⊥AC于F.
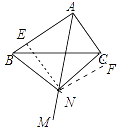
∵MA是∠BAC的平分线,
∴NE=NF,
在Rt△NEB和Rt△NFC中,
![]() ,
,
∴△NEB≌△NFC,
∴BE=CF,∠BNE=∠CNF,
易知四边形AENF是正方形,
∴AE=AF,∠BNC=∠ENF=90°,
∴△BNC是等腰直角三角形.
②∵AB+AC=(AE+BE)+(AF﹣CF)=2AE=18,
∴AE=AF=9,
∵△NEB≌△NFC,
∴S△NEB=S△NFC,
∴S四边形ABNC=S正方形AENF=92=81
【解析】(1)结论:判断3正确.只要证明四边形AEDF是正方形即可解决问题.(2)①△BCN是等腰直角三角形.如图作NE⊥AB于E,FN⊥AC于F.只要证明△NEB≌△NFC,四边形AENF是正方形即可解决问题.②由△NEB≌△NFC,推出S△NEB=S△NFC , 推出S四边形ABNC=S正方形AENF , 由此即可解决问题.


 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】北京时间5月27日,蛟龙号载人潜水器在太平洋马里亚纳海沟作业区开展了本航段第3次下潜,最大下潜深度突破6500米,数6500用科学记数法表示为( )
A.65×102
B.6.5×102
C.6.5×103
D.6.5×104
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B,C,D,E,F六个足球队进行单循环赛,当比赛进行到某一天时,统计出A,B,C,D,E五队已分别比赛了5,4,3,2,1场球,由此可知,还没有与B队比赛的球队是( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正比例函数y=kx(k>0)与反比例函数y= ![]() 的图象分别交于A、C两点,已知点B与点D关于坐标原点O成中心对称,且点B的坐标为(m,0).其中m>0.
的图象分别交于A、C两点,已知点B与点D关于坐标原点O成中心对称,且点B的坐标为(m,0).其中m>0.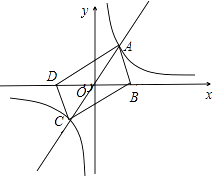
(1)四边形ABCD的是 . (填写四边形ABCD的形状)
(2)当点A的坐标为(n,3)时,四边形ABCD是矩形,求m,n的值.
(3)试探究:随着k与m的变化,四边形ABCD能不能成为菱形?若能,请直接写出k的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,D为AB上一点,以CD为直径的⊙O交BC于点E,连接AE交CD于点P,交⊙O于点F,连接DF,∠CAE=∠ADF.
(1)判断AB与⊙O的位置关系,并说明理由;
(2)若PF:PC=1:2,AF=5,求CP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查最适合用查阅资料的方法收集数据的是( )
A. 班级推选班长 B. 本校学生的到时间
C. 2014世界杯中,谁的进球最多 D. 本班同学最喜爱的明星
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com