
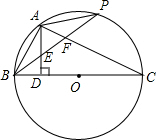
 如图,BC为⊙O的直径,AD⊥BC于点D,P是$\widehat{AC}$上的动点,连接PB分别交AD,AC于点E,F.
如图,BC为⊙O的直径,AD⊥BC于点D,P是$\widehat{AC}$上的动点,连接PB分别交AD,AC于点E,F.分析 (1)由圆周角定理知:AB⊥AC,在Rt△ABC中,AD⊥BC,易证得∠BAD=∠C,已知PA=AB,可得∠ABE=∠C,所以∠ABE=∠BAD,即AE=BE;
(2)当AF=EF时,∠FAE=∠FEA,易得∠FAE=∠ABD,∠FEA=∠DEB,因此∠BED=∠ABD,那么它们的余角也相等,即∠FBC=∠BAD,由(1)知∠BAD=∠C,即∠FBC=∠C,那么弧PC=弧AB,因此当弧PC=弧AB时,AF=EF.
解答 (1)证明:∵BC为⊙O的直径,
∴AB⊥AC,
又∵AD⊥BC,
∴∠BAD+∠DAC=∠C+∠DAC=90°,
∴∠BAD=∠C,
∵AB=AP,
∴∠ABE=∠C,
∴∠ABE=∠BAD.
∴AE=BE;
(2)当弧PC=弧AB时,AF=EF,
证明:∵弧PC=弧AB,
∴∠PBC=∠C,
∴90°-∠PBC=90°-∠C,
即∠BED=∠DAC,
∵∠BED=∠AEF,
∴∠DAC=∠AEF,
∴AF=EF.
点评 主要考查了圆中的有关性质,掌握其中的圆周角定理、圆心角、弧、圆周角之间的关系是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
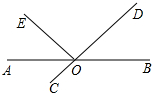 如图,直线AB,CD相交于点O,OA平分∠EOC.
如图,直线AB,CD相交于点O,OA平分∠EOC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
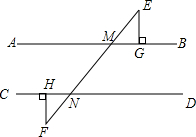 如图,直线EF和AB,CD分别相交于点M,N,EG⊥AB,FH⊥CD,垂足分别为G,H,且∠BME=53°,∠F=37°,试利用“三角形内角和等于180°”说明直线AB∥CD,EG∥FH.
如图,直线EF和AB,CD分别相交于点M,N,EG⊥AB,FH⊥CD,垂足分别为G,H,且∠BME=53°,∠F=37°,试利用“三角形内角和等于180°”说明直线AB∥CD,EG∥FH.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知数轴上有A,B,C三个点,它们表示的数分别是-24,-10,50.动点P,Q在数轴上运动,P,Q的运动速度分别是每秒3个单位长度和每秒4个单位长度.
如图,已知数轴上有A,B,C三个点,它们表示的数分别是-24,-10,50.动点P,Q在数轴上运动,P,Q的运动速度分别是每秒3个单位长度和每秒4个单位长度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com