
【题目】如图,在直角坐标平面中,O为原点,点A的坐标为(20,0),点B在第一象限内,BO=10,sin∠BOA= ![]() .
. 
(1)在图中,求作△ABO的外接圆(尺规作图,不写作法但需保留作图痕迹);
(2)求点B的坐标与cos∠BAO的值;
(3)若A,O位置不变,将点B沿x轴向右平移使得△ABO为等腰三角形,请求出平移后点B的坐标.
【答案】
(1)解:如图所示:
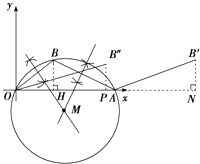
(2)解:如图,作BH⊥OA,垂足为H,
在Rt△OHB中,∵BO=10,sin∠BOA= ![]() ,
,
∴BH=6,
∴OH=8,∴点B的坐标为(8,6),
∵OA=20,OH=8,∴AH=12,
在Rt△AHB中,∵BH=6,
∴AB= ![]() =6
=6 ![]()
∴cos∠BAO= ![]()
(3)解:①当BO=AB时,∵AO=20,∴OH=10,
∴点B沿x轴正半轴方向平移2个单位,
②当AO=AB′时,∵AO=20,∴AB′=20,
过B′作B′N⊥x轴,
∵点B的坐标为(8,6),
∴B′N=6,∴AN= ![]() =2
=2 ![]() .
.
∴点B沿x轴正半轴方向平移(2 ![]() +12)个单位,
+12)个单位,
③当AO=OB″时,
∵AO=20,
∴OB″=20,
过B″作B″P⊥x轴.
∵B的坐标为(8,6),
∴B″P=6,
∴OP= ![]() =2
=2 ![]() ,
,
∴点B沿x轴正半轴方向平移(2 ![]() ﹣8)个单位,
﹣8)个单位,
综上所述当点B沿x轴正半轴方向平移2个单位、(2 ![]() +12)个单位,或(2
+12)个单位,或(2 ![]() ﹣8)个单位时,△ABO为等腰三角形
﹣8)个单位时,△ABO为等腰三角形
【解析】(1)作OB,AB的垂直平分线交于一点M,以点M为圆心,MA为半径画圆,则圆M即为所求;(2)如图,作BH⊥OA,垂足为H,在Rt△OHB中,由BO=10,sin∠BOA= ![]() ,得到BH=6,OH=8,求出点B的坐标为(8,6),根据OA=20,OH=8,求出AH=12,在Rt△AHB中,由BH=6,得到AB=
,得到BH=6,OH=8,求出点B的坐标为(8,6),根据OA=20,OH=8,求出AH=12,在Rt△AHB中,由BH=6,得到AB= ![]() =6
=6 ![]() ,求出cos∠BAO=
,求出cos∠BAO= ![]() ;(3)①当BO=AB时,由AO=20,得到OH=10,点B沿x轴正半轴方向平移2个单位;②当AO=AB′时,由AO=20,得到AB′=20,过B′作B′N⊥x轴,由点B的坐标为(8,6),得到B′N=6,AN=
;(3)①当BO=AB时,由AO=20,得到OH=10,点B沿x轴正半轴方向平移2个单位;②当AO=AB′时,由AO=20,得到AB′=20,过B′作B′N⊥x轴,由点B的坐标为(8,6),得到B′N=6,AN= ![]() =2
=2 ![]() .求得点B沿x轴正半轴方向平移(2
.求得点B沿x轴正半轴方向平移(2 ![]() +12)个单位,③当AO=OB″时,由AO=20,得到OB″=20,过B″作B″P⊥x轴.由B的坐标为(8,6),得到B″P=6,OP=
+12)个单位,③当AO=OB″时,由AO=20,得到OB″=20,过B″作B″P⊥x轴.由B的坐标为(8,6),得到B″P=6,OP= ![]() =2
=2 ![]() ,点B沿x轴正半轴方向平移(2
,点B沿x轴正半轴方向平移(2 ![]() ﹣8)个单位.
﹣8)个单位.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,射线OA表示的方向是北偏东15°,射线OB表示的方向是北偏西40°.
(1)若∠AOC=∠AOB,则射线OC表示的方向是 ;
(2)若射线OD是射线OB的反向延长线,则射线OD表示的方向是 ;
(3)∠BOD可以看作是由OB绕点O逆时针方向旋转至OD形成的角,作∠BOD的平分线OE;
(4)在(1),(2),(3)的条件下,求∠COE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分别与⊙O相切于E,F,G三点,过点D作⊙O的切线BC于点M,切点为N,则DM的长为( ) 
A.![]()
B.![]()
C.![]()
![]()
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)【问题情境】
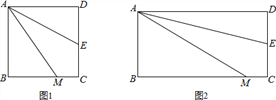
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.
【探究展示】(1)证明:AM=AD+MC;
【拓展延伸】(2)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)中的结论是否成立?请作出判断,不需要证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,水坝的横断面是梯形,背水坡AB的坡角∠BAD=60°,坡长AB=20 ![]() m,为加强水坝强度,降坝底从A处后水平延伸到F处,使新的背水坡角∠F=45°,求AF的长度(结果精确到1米,参考数据:
m,为加强水坝强度,降坝底从A处后水平延伸到F处,使新的背水坡角∠F=45°,求AF的长度(结果精确到1米,参考数据: ![]() 1.414,
1.414, ![]() ≈1.732).
≈1.732).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,∠B=60°,△AB′C′可以由△ABC绕点A顺时针旋转90°得到(点B′与点B是对应点,点C′与点C是对应点),连接CC′,则∠CC′B′的度数是 . 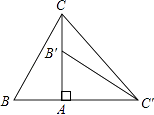
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程
(1)x2=49
(2)3x2-7x=0
(3)![]() (直接开平方法)
(直接开平方法)
(4)![]() (用配方法)
(用配方法)
(5)![]() (因式分解法)
(因式分解法)
(6)![]()
(7)(x-2)(x-5)=-2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线与x交于A(﹣1,0)、E(3,0)两点,与y轴交于点B(0,3).
(1)求抛物线的解析式;
(2)设抛物线顶点为D,求四边形AEDB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,已知点C在线段AB上,且AC=6cm,BC=4cm,点M,N分别是AC,BC的中点,求线段MN的长度.
![]()
(2)在(1)中,如果AC=acm,BC=bcm,其它条件不变,你能猜出MN的长度吗?请你用一句简洁的话表述你发现的规律.
(3)对于(1)题,如果我们这样叙述它:“已知线段AC=6cm,BC=4cm,点C在直线AB上,点M,N分别是AC,BC的中点,求MN的长度.”结果会有变化吗?如果有,求出结果.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com