
【题目】如图,射线OA表示的方向是北偏东15°,射线OB表示的方向是北偏西40°.
(1)若∠AOC=∠AOB,则射线OC表示的方向是 ;
(2)若射线OD是射线OB的反向延长线,则射线OD表示的方向是 ;
(3)∠BOD可以看作是由OB绕点O逆时针方向旋转至OD形成的角,作∠BOD的平分线OE;
(4)在(1),(2),(3)的条件下,求∠COE的度数.

【答案】(1)北偏东70° (2)南偏东40° (3)见解析(4)160°
【解析】
(1)先求出∠AOB=55°,再求得∠AOC的度数,即可确定OC的方向;
(2)由对顶角性质得∠FOD=40,可得射线OD表示的方向;
(3)通过作线段垂直平分线可得;
(4)根据射线OE平分∠BOD,即可求出∠DOE=90°再利用∠DOC=180-2×55°,求出答案即可.
(1)∵OB的方向是北偏西40°,OA的方向是北偏东15°,
∴∠NOB=40°,∠NOA=15°,
∴∠AOB=∠NOB+∠NOA=55°,
∵∠AOB=∠AOC,
∴∠AOC=55°,
∴∠NOC=∠NOA+∠AOC=70°,
∴OC的方向是北偏东70°;
(2) 由对顶角性质得∠FOD=∠NOB=40,可得射线OD表示的方向是:南偏东40°.
(3)如图
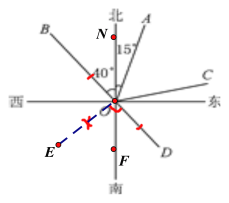
(4)∵∠AOB=55°,∠AOC=∠AOB,
∴∠BOC=110°.
又∵射线OD是OB的反向延长线,
∴∠BOD=180°.
∴∠COD=180°-110°=70°.
∵射线OE平分∠BOD,
∴∠DOE=90°.
∴∠COE=∠DOE+∠COD=90°+70°=160°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】“保护好环境,拒绝冒黑烟”.某市公交公司将淘汰某一条线路上“冒黑烟”较严重的公交车,计划购买A型和B型两种环保节能公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在该线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于680万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少总费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】骰子是一种特别的数字立方体(见右图),它符合规则:相对两面的点数之和总是7,下面四幅图中可以折成符合规则的骰子的是( )
![]()
A.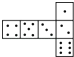 B.
B.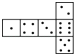 C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0) 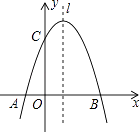
(1)求m的值及抛物线的顶点坐标.
(2)点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,BC⊥AF于点C,∠A+∠1=90°.
(1)求证:AB∥DE;
(2)如图2,点P从点A出发,沿线段AF运动到点F停止,连接PB,PE.则∠ABP,∠DEP,∠BPE三个角之间具有怎样的数量关系(不考虑点P与点A,D,C重合的情况)?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对下列代数式作出解释,其中不正确的是( )
A. a-b:今年小明b岁,小明的爸爸a岁,小明比他爸爸小(a-b)岁
B. a-b:今年小明b岁,小明的爸爸a岁,则小明出生时,他爸爸为(a-b)岁
C. ab:长方形的长为acm,宽为bcm,长方形的面积为ab ![]()
D. ab:三角形的一边长为acm,这边上的高为bcm,此三角形的面积为ab ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
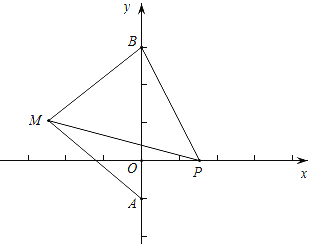
【题目】如图,在平面直角坐标系中,已知A(0,﹣1),B(0,3),点M为第二象限内一点,且点M的坐标为(t,1).
(1)请用含t的式子表示△ABM的面积;
(2)当t=﹣2时,在x轴的正半轴上有一点P,使得△BMP的面积与△ABM的面积相等,请求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
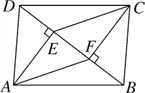
【题目】四边形ABCD中,AD=BC,BE=DF,AE⊥BD,CF⊥BD,垂足分别为点E,F.
(1)求证:△ADE≌△CBF;
(2)若AC与BD相交于点O,求证:AO=CO.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标平面中,O为原点,点A的坐标为(20,0),点B在第一象限内,BO=10,sin∠BOA= ![]() .
. 
(1)在图中,求作△ABO的外接圆(尺规作图,不写作法但需保留作图痕迹);
(2)求点B的坐标与cos∠BAO的值;
(3)若A,O位置不变,将点B沿x轴向右平移使得△ABO为等腰三角形,请求出平移后点B的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com