

分析 (1)根据角平分线的性质,可以证明本结论成立;
(2)①根据切线的性质可知AB=AM,根据勾股定理可以求得BC的长,进而可以求得圆的半径的长;
②根据题意可以求得AD的长,然后根据三角形相似可以求得DF的长,由等腰三角形的性质可以求得EF的长.
解答 (1)证明:∵∠ABC=90°,∠CAB的平分线是AO,
∴点O到AB和到AC的距离相等,
∴点O到AC的距离等于圆O的半径,
∴⊙O与AC相切;
(2)①作OM⊥AC于点M,如右图所示,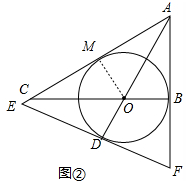
∵AB=6,AC=10,∠ABC=90°,
∴BC=8,AB=AM=6,
∴MC=4,OC=8-OB,
设圆O的半径是r,
∴r2+42=(8-r)2
解得,r=3,
即⊙O的半径是3;
②∵AB=6,BO=3,∠ABO=90°,
∴AO=$3\sqrt{5}$,
∴AD=3+3$\sqrt{5}$,
∵AD⊥EF,
∴∠ADF=90°,
∴∠ADF=∠ABO=90°,
∵∠DAF=∠BAO,
∴△DAF∽△BAO,
∴$\frac{AD}{DF}=\frac{AB}{BO}$,
即$\frac{3+3\sqrt{5}}{DF}=\frac{6}{3}$,
解得,DF=$\frac{3+3\sqrt{5}}{2}$,
∵AD平分∠EAF,AD⊥EF,
∴EF=2DF=3$+3\sqrt{5}$.
点评 本题考查切线的性质与判定,解题的关键是明确题意,找出所求问题需要的条件,利用勾股定理和三角形的相似解答.


科目:初中数学 来源: 题型:解答题
 如图,等边△ABC中,边长为5,D是BC上一点,∠EDF=60°.
如图,等边△ABC中,边长为5,D是BC上一点,∠EDF=60°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
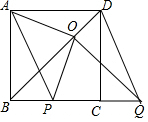 如图,BD是正方形ABCD的对角线,BC=2,边BC在其所在的直线上平移,经通过平移得到的线段记为PQ,连接PA、QD,并过点Q作QO⊥BD,垂足为O,连接OA、OP.
如图,BD是正方形ABCD的对角线,BC=2,边BC在其所在的直线上平移,经通过平移得到的线段记为PQ,连接PA、QD,并过点Q作QO⊥BD,垂足为O,连接OA、OP.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
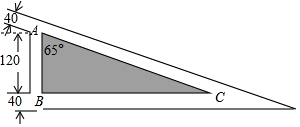 如图所示为某市生态绿化工程中的一幅大型绿化的平面图(单位:米)根据图示尺寸计算绿地(阴影部分-直角三角形)的面积(精确到0.1m)(参考数据sin65°=0.9063、cos65°=0.4226、tan65°=2.1445、cot65°=0.4663)
如图所示为某市生态绿化工程中的一幅大型绿化的平面图(单位:米)根据图示尺寸计算绿地(阴影部分-直角三角形)的面积(精确到0.1m)(参考数据sin65°=0.9063、cos65°=0.4226、tan65°=2.1445、cot65°=0.4663)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -b<a<b<-a | B. | -b<b<-a<a | C. | a<-b<b<-a | D. | -a<b<-b<a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com