
 如图,等边△ABC中,边长为5,D是BC上一点,∠EDF=60°.
如图,等边△ABC中,边长为5,D是BC上一点,∠EDF=60°.分析 (1)由等边△ABC中,∠EDF=60°,易得∠B=∠C=60°,继而求得∠BED=∠CDF,则可证得:△BDE∽△CFD;
(2)由等边△ABC中,边长为5,BD=1,可求得CD的长,然后由△BDE∽△CFD,根据相似三角形的对应边成比例,求得答案.
解答 (1)证明:∵△ABC是等边三角形,
∴∠B=∠C=60°,
∵∠EDF+∠CDF=∠B+∠BED,∠EDF=60°,
∴∠BED=∠CDF,
∴△BDE∽△CFD;
(2)解:∵等边△ABC中,边长为5,BD=1,
∴CD=BC-BD=4,
∵△BDE∽△CFD,
∴BE:CD=BD:CF,
∴BE:4=1:3,
∴BE=$\frac{4}{3}$.
点评 此题考查了相似三角形的判定与性质以及等边三角形的判定与性质.注意根据有两角对应相等的三角形相似证得△BDE∽△CFD是解此题的关键.


 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
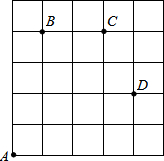 如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:A→B(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中
如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:A→B(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如右图,以数轴的单位长的线段为边作三个竖立的正方形,以数轴的原点为圆心,OP的长为半径画弧,交数轴于点A,则点A表示的数是-$\sqrt{10}$.
如右图,以数轴的单位长的线段为边作三个竖立的正方形,以数轴的原点为圆心,OP的长为半径画弧,交数轴于点A,则点A表示的数是-$\sqrt{10}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
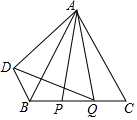 如图,△ABC是等边三角形,AB=3cm,动点P、Q分别从点B,C同时出发,运动速度均为2cm/s,点P从B点出发,沿B→C运动,到点C停止,点Q从点C出发,沿C→B运动,到点B停止,连接AP、AQ,点P关于直线AB的对称点为D,连接BD、DQ,设点P的运动时间为t(s).
如图,△ABC是等边三角形,AB=3cm,动点P、Q分别从点B,C同时出发,运动速度均为2cm/s,点P从B点出发,沿B→C运动,到点C停止,点Q从点C出发,沿C→B运动,到点B停止,连接AP、AQ,点P关于直线AB的对称点为D,连接BD、DQ,设点P的运动时间为t(s).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com