
【题目】如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动,4秒后,两点相距16个单位长度.已知点B的速度是点A的速度的3倍(速度单位:单位长度/秒).
(1)求出点A、点B运动的速度,并在数轴上标出A、B两点从原点出发运动4秒时的位置;
(2)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动,再过几秒时,原点恰好处在AB的中点?
(3)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动时,另一点C同时从原点O位置出发向B点运动,且C的速度是点A的速度的一半;当点C运动几秒时,C为AB的中点?![]()
【答案】
(1)解:设A的速度是x,则B的速度为3x,由题意,
得:4(x+3x)=16,解得:x=1,
∴A的速度是1单位长度/秒,B的速度为2单位长度/秒,
∴A到达的位置为-4,B到达的位置是12,在数轴上的位置如图:
![]()
答:A的速度为1单位长度/秒;B的速度为2单位长度/秒;
(2)解:设y秒后,原点恰好在A、B的正中间,由题意,得:12-3y=y+4,y=2.
答:再过2秒时,原点恰好处在AB的中点
(3)解:设当C运动z秒后,C为AB的中点,由题意得:4+z+ ![]() z=12-3z-
z=12-3z-![]() z,
z,
解得:z= ![]() .
.
答:当C运动 ![]() 秒时,C为AB的中点.
秒时,C为AB的中点.
【解析】(1)设A的速度是x,则B的速度为3x, 根据4秒后,两点相距16个单位长度列出方程,求解即可;
(2)设y秒后,原点恰好在A、B的正中间,则A离原点的距离为y+4,B离原点的距离为12-3y ,根据A离原点的距离=B离原点的距离列出方程,求解即可;
(3)设当C运动z秒后,C为AB的中点,则A离C点的距离为4+z+ ![]() z ,B离C点的距离为12-3z-
z ,B离C点的距离为12-3z-![]() z, 根据A离C的距离=B离C的距离列出方程,求解即可.
z, 根据A离C的距离=B离C的距离列出方程,求解即可.


科目:初中数学 来源: 题型:
【题目】如图,已知射线CD∥OA,点E、点F是OA上的动点,CE平分∠OCF,且满足∠FCA=∠FAC.
(1)若∠O=∠ADC,判断AD与OB的位置关系,证明你的结论.
(2)若∠O=∠ADC=60°,求∠ACE的度数.
(3)在(2)的条件下左右平行移动AD,∠OEC和∠CAD存在怎样的数量关系?请直接写出结果(不需写证明过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,真命题是( )
A. 两条对角线互相平分的四边形是平行四边形
B. 两条对角线互相垂直的四边形是菱形
C. 两条对角线互相垂直且相等的四边形是正方形
D. 两条对角线相等的四边形是矩形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小彬是学校的篮球队长,在一场篮球比赛中,他一人得了25分,其中罚球得了5分,他投进的2分球比3分球多5个,则他本场比赛3分球进了( )
A. 1个
B. 2个
C. 3个
D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
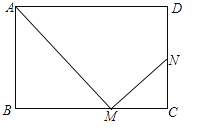
【题目】在矩形ABCD中,AB=a,AD=b,点M为BC边上一动点(点M与点B、C不重合),连接AM,过点M作MN⊥AM,垂足为M,MN交CD或CD的延长线于点N.
(1)求证:△CMN∽△BAM;
(2)设BM=x,CN=y,求y关于x的函数解析式.当x取何值时,y有最大值,并求出y的最大值;
(3)当点M在BC上运动时,求使得下列两个条件都成立的b的取值范围:①点N始终在线段CD上,②点M在某一位置时,点N恰好与点D重合.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B两地有公路和铁路相连,在这条路上有一家食品厂,它到B地的距离是到A地的2倍,这家工厂从A地购买原料,制成食品卖到B地.已知公路运价为1.5元/(公里吨),铁路运价为1元/(公里吨),这两次运输(第一次:A地→食品厂,第二次:食品厂→B地)共支出公路运费15600元,铁路运费20600元.![]()
问:
(1)这家食品厂到A地的距离是多少?
(2)这家食品厂此次共买进原料和卖出食品各多少吨?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com