
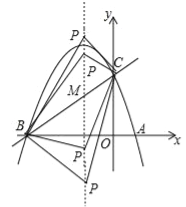
【题目】如图,已知抛物线![]() (a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.

【答案】(1)y=x+3,![]() ;(2)M(﹣1,2);(3)P(﹣1,﹣2)或(﹣1,4)或(﹣1,
;(2)M(﹣1,2);(3)P(﹣1,﹣2)或(﹣1,4)或(﹣1,![]() ) 或(﹣1,
) 或(﹣1,![]() ).
).
【解析】(1)依题意得: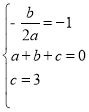 ,解得:
,解得: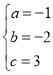 ,∴抛物线解析式为
,∴抛物线解析式为![]() .
.
∵对称轴为x=﹣1,且抛物线经过A(1,0),∴把B(﹣3,0)、C(0,3)分别代入直线y=mx+n,得![]() ,解得:
,解得:![]() ,∴直线y=mx+n的解析式为y=x+3;
,∴直线y=mx+n的解析式为y=x+3;
(2)设直线BC与对称轴x=﹣1的交点为M,则此时MA+MC的值最小.
把x=﹣1代入直线y=x+3得,y=2,∴M(﹣1,2),即当点M到点A的距离与到点C的距离之和最小时M的坐标为(﹣1,2);
(3)设P(﹣1,t),又∵B(﹣3,0),C(0,3),∴![]() =18,
=18,![]() =
=![]() =
=![]() ,
,![]() =
=![]() =
=![]() ;
;
①若点B为直角顶点,则![]() ,即:
,即:![]() 解之得:t=﹣2;
解之得:t=﹣2;
②若点C为直角顶点,则![]() ,即:
,即:![]() ,解之得:t=4;
,解之得:t=4;
③若点P为直角顶点,则![]() ,即:
,即:![]() ,解之得:
,解之得:![]() ,
,![]() ;
;
综上所述P的坐标为(﹣1,﹣2)或(﹣1,4)或(﹣1,![]() ) 或(﹣1,
) 或(﹣1,![]() ).
).


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OCDE的顶点C和E分别在y轴的正半轴和x轴的正半轴上,OC=8,OE=17,抛物线![]() 与y轴相交于点A,抛物线的对称轴与x轴相交于点B,与CD交于点K.
与y轴相交于点A,抛物线的对称轴与x轴相交于点B,与CD交于点K.
(1)将矩形OCDE沿AB折叠,点O恰好落在边CD上的点F处.
①点B的坐标为( 、 ),BK的长是 ,CK的长是 ;
②求点F的坐标;
③请直接写出抛物线的函数表达式;
(2)将矩形OCDE沿着经过点E的直线折叠,点O恰好落在边CD上的点G处,连接OG,折痕与OG相交于点H,点M是线段EH上的一个动点(不与点H重合),连接MG,MO,过点G作GP⊥OM于点P,交EH于点N,连接ON,点M从点E开始沿线段EH向点H运动,至与点N重合时停止,△MOG和△NOG的面积分别表示为S1和S2,在点M的运动过程中,S1S2(即S1与S2的积)的值是否发生变化?若变化,请直接写出变化范围;若不变,请直接写出这个值.
温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,OA⊥OC,OB⊥OD,下面结论中,其中说法正确的是( ) 
①∠AOB=∠COD;②∠AOB+∠COD=90°;③∠BOC+∠AOD=180°;④∠AOC-∠COD=∠BOC.
A.①②③
B.①②④
C.①③④
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD,
(1)图中除直角外,还有相等的角吗?请写出两对:①;② .
(2)如果∠AOD=40°,则①∠BOC=;②OP是∠BOC的平分线,所以∠COP=;
③求∠BOF的度数 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com