
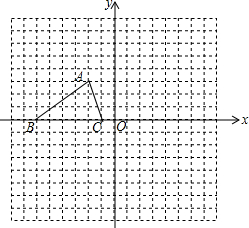
 如图,已知△ABC三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).
如图,已知△ABC三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).分析 (1)利用中心对称的性质画出点A和B的对称点D和E点,再写出D点坐标;
(2)利用网格特点和旋转的性质画出点A、B、C的对应点A′、B′、C′,从而得到△A′B′C,再写出A′点的坐标;
(3)根据旋转的性质得AC⊥A′C′,而点A和点D关于C点对称,则AD⊥A′C′,设AD交A′C′于F,证明Rt△DFC′∽Rt△DOC,利用相似比可计算出DF=$\frac{3\sqrt{10}}{5}$,FC′=$\frac{\sqrt{10}}{5}$,则根据三角形的面积公式计算S△FDC′即可.
解答 解:(1)如图,△DEC为所作,点D的坐标为(0,-3);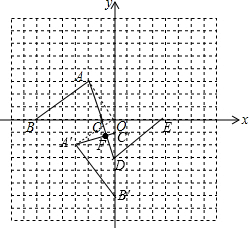
(2)如图,△A′B′C为所作,点A′坐标为(-3,-2);
(3)∵△ABC绕坐标原点O逆时针旋转90°得△A′B′C,
∴AC⊥A′C′,
∵点A和点D关于C点对称,
∴点D在AC的延长线上,
∴AD⊥A′C′,
设AD交A′C′于F,
OC=1,OD=3,DC′=2,CD=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
∵∠FDC′=∠ODC,
∴Rt△DFC′∽Rt△DOC,
∴$\frac{DF}{OD}$=$\frac{FC′}{OC}$=$\frac{DC′}{DC}$,即$\frac{DF}{3}$=$\frac{FC′}{1}$=$\frac{2}{\sqrt{10}}$,
∴DF=$\frac{3\sqrt{10}}{5}$,FC′=$\frac{\sqrt{10}}{5}$,
∴S△DFC′=$\frac{1}{2}$×$\frac{3\sqrt{10}}{5}$×$\frac{\sqrt{10}}{5}$=$\frac{3}{5}$.
即△CDE与△A′B′C′重叠部分的面积为$\frac{3}{5}$.
故答案为(0,-3),(-3,-2),$\frac{3}{5}$.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了相似三角形的判定与性质.


科目:初中数学 来源: 题型:选择题
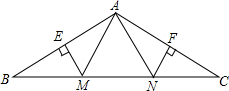 如图所示,在等腰△ABC中,∠BAC=120°,若EM和FN分别垂直平分AB和AC,垂足分别为E、F、M、N都在BC边上,且EM=FN=4,则BC的长度为( )
如图所示,在等腰△ABC中,∠BAC=120°,若EM和FN分别垂直平分AB和AC,垂足分别为E、F、M、N都在BC边上,且EM=FN=4,则BC的长度为( )| A. | 12 | B. | 16 | C. | 20 | D. | 24 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一辆火车从百货大楼出发负责送货,向东走了4千米到达小明家,继续向东走了1.5千米到达小红家,然后向西走了8.5千米到达小刚家,最后返回百货大楼.
一辆火车从百货大楼出发负责送货,向东走了4千米到达小明家,继续向东走了1.5千米到达小红家,然后向西走了8.5千米到达小刚家,最后返回百货大楼.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,一个高为1m的油筒内有油,一根木棒长1.2m,从桶盖小口斜插入桶内,一端到底部,另一端正好到小口,抽出木棒,量得棒上浸油部分的长0.36m,则桶内油的高度为( )
如图,一个高为1m的油筒内有油,一根木棒长1.2m,从桶盖小口斜插入桶内,一端到底部,另一端正好到小口,抽出木棒,量得棒上浸油部分的长0.36m,则桶内油的高度为( )| A. | 0.28m | B. | 0.385m | C. | 0.4m | D. | 0.3m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com