
分析 先解不等式组,求得x的值,根据运算顺序,先算括号里面的,分子、分母分别有理化,再约分即可,把x的值代入计算即可.
解答 解:解不等式得,-1<x<2,
则x=0或1,
原式=$\frac{(x-4)^{2}}{x(x+2)}$×$\frac{x+2}{(4+x)(4-x)}$+$\frac{1}{x+4}$
=$\frac{4-x}{x(x+4)}$+$\frac{1}{x+4}$
=$\frac{4}{x(x+4)}$
当x=0时,原式无意义,
当x=1时,原式=$\frac{4}{5}$.
点评 本题考查了分式的化简求值,解这类题的关键是利用分解因式的方法化简分式,特别注意运算顺序及符号的处理.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:解答题
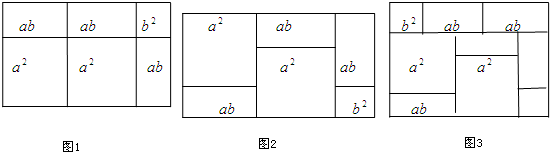
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售时段 | A种配餐销售量 | B种配餐销售量 | 销售额 |
| 第一周 | 100份 | 300份 | 5500元 |
| 第二周 | 200份 | 400份 | 8000元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
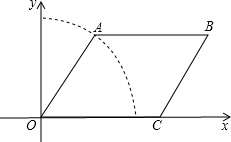 如图,点A是以O为圆心的圆上的一个动点,点C是x轴正半轴上的一个动点,BC∥OA,AB∥x轴.
如图,点A是以O为圆心的圆上的一个动点,点C是x轴正半轴上的一个动点,BC∥OA,AB∥x轴.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
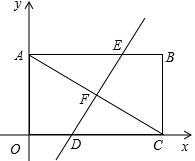 如图,平面直角坐标系中,矩形OABC的对角线AC=10,边OA=6.
如图,平面直角坐标系中,矩形OABC的对角线AC=10,边OA=6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
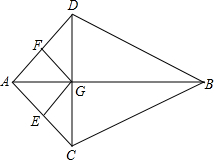 如图,AB是CD的垂直平分线,交CD于点G,过点G分别作GE⊥AC于E,GF⊥AD于F
如图,AB是CD的垂直平分线,交CD于点G,过点G分别作GE⊥AC于E,GF⊥AD于F查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com