
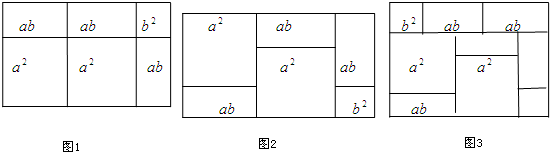
 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��
���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
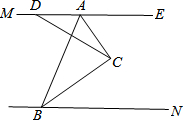 ��ͼ����֪MA��NB��CAƽ�֡�BAE��CBƽ�֡�ABN����D������AM��һ���㣬��DC����D��������AM��������A�㣩�ϻ���ʱ����ADC+��ACD+ABC�Ķ����Ƿ����仯�������䣬˵�����ɣ������������
��ͼ����֪MA��NB��CAƽ�֡�BAE��CBƽ�֡�ABN����D������AM��һ���㣬��DC����D��������AM��������A�㣩�ϻ���ʱ����ADC+��ACD+ABC�Ķ����Ƿ����仯�������䣬˵�����ɣ�������������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
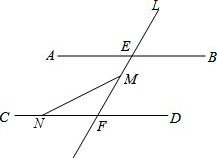 ��ͼ��AB��CD��ֱL��AB��CD�ֱ��ڵ�E��F����M���߶�EF�ϣ���M����E��F�غϣ���N��ֱ��CD�ϵ�һ�����㣨��N����F�غϣ�
��ͼ��AB��CD��ֱL��AB��CD�ֱ��ڵ�E��F����M���߶�EF�ϣ���M����E��F�غϣ���N��ֱ��CD�ϵ�һ�����㣨��N����F�غϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
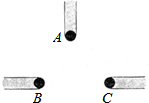 ��1����ͼ��С�գ�A����С����B����С�£�C�������Ǹ���Ӱ�ӵĸ���ͼ�����������������ε��ε��ڲ���һյ·�ƣ�����Ϊ��ͼ���ڰ��������µĸ���ͼ������������յ·���µĸ���ͼ��
��1����ͼ��С�գ�A����С����B����С�£�C�������Ǹ���Ӱ�ӵĸ���ͼ�����������������ε��ε��ڲ���һյ·�ƣ�����Ϊ��ͼ���ڰ��������µĸ���ͼ������������յ·���µĸ���ͼ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
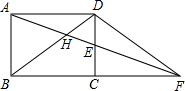 ��ͼ������ABCD�У�EΪCD���е㣬����AE���ӳ���BC���ӳ����ڵ�F������BD��AF��H��AD=10$\sqrt{2}$����tan��EFC=$\frac{\sqrt{2}}{4}$����ôAH�ij�Ϊ��������
��ͼ������ABCD�У�EΪCD���е㣬����AE���ӳ���BC���ӳ����ڵ�F������BD��AF��H��AD=10$\sqrt{2}$����tan��EFC=$\frac{\sqrt{2}}{4}$����ôAH�ij�Ϊ��������| A�� | $\frac{10\sqrt{6}}{3}$ | B�� | 5$\sqrt{2}$ | C�� | 10 | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
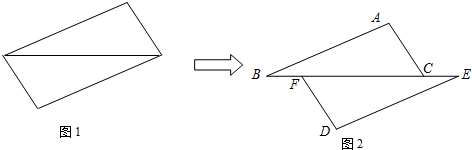
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com