
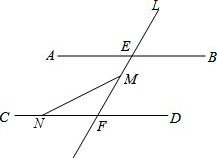
 如图,AB∥CD,直L交AB、CD分别于点E、F,点M在线段EF上(点M不与E、F重合),N是直线CD上的一个动点(点N不与F重合)
如图,AB∥CD,直L交AB、CD分别于点E、F,点M在线段EF上(点M不与E、F重合),N是直线CD上的一个动点(点N不与F重合)分析 (1)利用两直线平行,同旁内角互补和三角形的内角和为180°,易得∠FMN+∠FNM=∠AEF;
(2)根据两直线平行,内错角相等和三角形的内角和为180度,易得∠FMN+∠FNM+∠AEF=180°.
解答 解:(1)∵AB∥CD,
∴∠AEF+∠MFN=180°.
∵∠MFN+∠FMN+∠FNM=180°,
∴∠FMN+∠FNM=∠AEF.
(2)∠FMN+∠FNM+∠AEF=180°.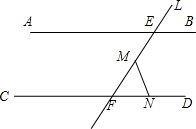
理由:如图所示,
∵AB∥CD,
∴∠AEF=∠MFN.
∵∠MFN+∠FMN+∠FNM=180°,
∴∠FMN+∠FNM+∠AEF=180°.
点评 本题考查的是平行线的判定与性质,用到的知识点为:两直线平行,同旁内角互补.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:解答题
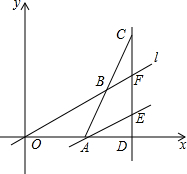 如图,在平面直角坐标系中,点A的坐标为(3,0),直线l与x轴正半轴夹角为30°,点B为直线l上的一个动点,延长AB至点C,使得AB=BC,过点C作CD⊥x轴于点D,交直线l于点F,过点A作AE∥l交直线CD于点E.
如图,在平面直角坐标系中,点A的坐标为(3,0),直线l与x轴正半轴夹角为30°,点B为直线l上的一个动点,延长AB至点C,使得AB=BC,过点C作CD⊥x轴于点D,交直线l于点F,过点A作AE∥l交直线CD于点E.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
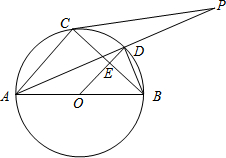 如图,⊙O是以AB为直径的△ABC的外接圆,点D是劣弧$\widehat{BC}$的中点,连结AD并延长,与过C点的直线交于P,OD与BC相交于点E.
如图,⊙O是以AB为直径的△ABC的外接圆,点D是劣弧$\widehat{BC}$的中点,连结AD并延长,与过C点的直线交于P,OD与BC相交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
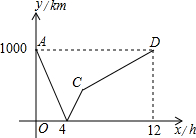 如图所示,一列快车从甲地开往乙地,一列慢车从乙地开往甲地,两车同时出发,设慢车行驶的时间为x小时,两车之间的距离为y千米,图中的折线表示y与x之间的函数关系,则快车的速度是$166\frac{2}{3}$千米/小时.
如图所示,一列快车从甲地开往乙地,一列慢车从乙地开往甲地,两车同时出发,设慢车行驶的时间为x小时,两车之间的距离为y千米,图中的折线表示y与x之间的函数关系,则快车的速度是$166\frac{2}{3}$千米/小时.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
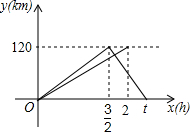 一辆轿车从甲地驶往乙地,到达乙地后立即返回甲地,速度是原来的1.5倍,往返共用t小时;一辆货车同时从甲地驶往乙地,到达乙地后停止,两车同时出发,匀速行驶,设轿车行驶的时间为x(h),两车离开甲地的距离为y(km),两车行驶过程中y与x之间的函数图象如图所示.
一辆轿车从甲地驶往乙地,到达乙地后立即返回甲地,速度是原来的1.5倍,往返共用t小时;一辆货车同时从甲地驶往乙地,到达乙地后停止,两车同时出发,匀速行驶,设轿车行驶的时间为x(h),两车离开甲地的距离为y(km),两车行驶过程中y与x之间的函数图象如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com