
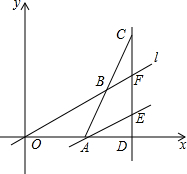
 如图,在平面直角坐标系中,点A的坐标为(3,0),直线l与x轴正半轴夹角为30°,点B为直线l上的一个动点,延长AB至点C,使得AB=BC,过点C作CD⊥x轴于点D,交直线l于点F,过点A作AE∥l交直线CD于点E.
如图,在平面直角坐标系中,点A的坐标为(3,0),直线l与x轴正半轴夹角为30°,点B为直线l上的一个动点,延长AB至点C,使得AB=BC,过点C作CD⊥x轴于点D,交直线l于点F,过点A作AE∥l交直线CD于点E.分析 (1)把x=6代入直线OB解析式求出y的值,确定出B坐标,根据B为AC中点,求出C的坐标,再由AE与OB平行确定出直线AE解析式,由CD垂直于x轴,得到E与C横坐标相同,把C横坐标代入直线AE解析式求出E的纵坐标,即为DE的长;
(2)在点B的运动过程中,线段CF的长度不发生改变,设B横坐标为a,代入直线OB解析式表示出纵坐标,根据B为AC中点,表示出C的坐标,再由AE与OB平行确定出直线AE解析式,由CD垂直于x轴,得到E与C横坐标相同,把C横坐标代入直线AE解析式表示出E的纵坐标,由CD-DE求出CE的长,根据F为CE中点,求出CF的长即可;
(3)分当点D在点A的右侧时、当点D在线段OA上时和当点D在点O的左侧时三种情况分类讨论即可.
解答 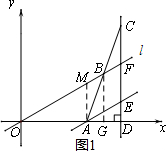 解:(1)∵直线l与x轴正半轴夹角为30°,
解:(1)∵直线l与x轴正半轴夹角为30°,
∴直线l的解析式为y=$\frac{\sqrt{3}}{3}x$,
把x=6代入y=$\frac{\sqrt{3}}{3}x$得:y=2$\sqrt{3}$,
∵A(3,0),B(6,2$\sqrt{3}$),且B为AC中点,
∴C(9,4$\sqrt{3}$),
由AE∥OB,且直线OB解析式为y=$\frac{\sqrt{3}}{3}x$,故设直线AE解析式为y=$\frac{\sqrt{3}}{3}x$+b,
把A(3,0)代入得:b=-$\sqrt{3}$,即直线AE解析式为y=$\frac{\sqrt{3}}{3}x$-$\sqrt{3}$,
由CD⊥x轴,得到C与E横坐标相同,
把x=9代入直线AE解析式得:y=2$\sqrt{3}$,
则DE=2$\sqrt{3}$;
故答案为:C(9,$4\sqrt{3}$),DE=$2\sqrt{3}$;
(2)如图(1),过点A作AM⊥x轴于M,
∴∠OAM=90°,∠BOA=30°,
∴AM=OAtan∠BOA=$\sqrt{3}$.
∵B为AC的中点,
∴AB=BC
又∵AM∥CF,
∴∠AMB=∠CFB,∠MAB=∠FCB
∴△ABM≌△CBF
∴CF=AM=$\sqrt{3}$.
∴线段CF的长度保持不变. 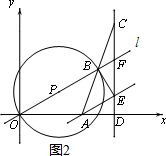
(3)如图1,过点B作BG⊥x轴于点G.
易证,OB=2BG,CD=2BG,
∴OB=CD.
( I)当点D在点A的右侧时,⊙P只能与BE相切,如图2
设DE=a,则OB=CD=$2\sqrt{3}+a$.
∵⊙P与BE相切于点B,
∴OB⊥BE.
易得BF=$\frac{1}{2}$EF=$\frac{{\sqrt{3}}}{2}$.
∴OF=OB+BF=$\frac{5}{2}\sqrt{3}+a$.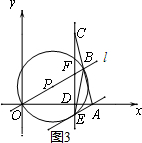 ∴OF=2DF,
∴OF=2DF,
∴$\frac{5}{2}\sqrt{3}+a$=$2({\sqrt{3}+a})$.
解得$a=\frac{{\sqrt{3}}}{2}$
∴DE=$\frac{{\sqrt{3}}}{2}$.
( II)当点D在线段OA上时,
①若⊙P与直线AE相切,如图3,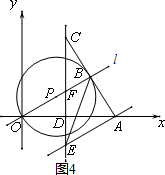 易得,直线l与AE的距离是$\frac{3}{2}$.
易得,直线l与AE的距离是$\frac{3}{2}$.
∴OB=3.
∴CD=3.
∴DE=2CF-CD=$2\sqrt{3}-3$.
②当⊙P与AB相切,如图4.
∴∠OBA=90°.
∴OB=OAtan∠OBA=$\frac{3}{2}\sqrt{3}$.
∴CD=$\frac{3}{2}\sqrt{3}$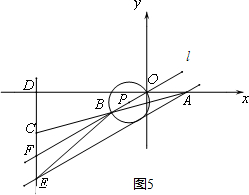 ∴DE=2CF-CD=$2\sqrt{3}-\frac{3}{2}\sqrt{3}$=$\frac{{\sqrt{3}}}{2}$.
∴DE=2CF-CD=$2\sqrt{3}-\frac{3}{2}\sqrt{3}$=$\frac{{\sqrt{3}}}{2}$.
(III)当点D在点O的左侧时,⊙P只能与直线AE相切,如图5
∵直线l与AE的距离是$\frac{3}{2}$,
∴OB=3.
∴CD=3.
∴DE=2CF+CD=$2\sqrt{3}+3$.
综上所述,DE的长为$\frac{{\sqrt{3}}}{2}$或$2\sqrt{3}-3$或$2\sqrt{3}+3$.
点评 此题属于一次函数综合题,涉及的知识有:两直线平行时斜率满足的关系,两直线垂直时斜率满足的关系,坐标与图形性质,待定系数法求一次函数解析式,利用了分类讨论的思想,熟练掌握一次函数的性质是解本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
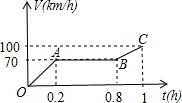 一辆摩托车从起点出发沿笔直的赛道向终点行驶,行驶中的速度V(km/h)与时间t(h)的关系部分信息如图所示,根据图象有下列说法:
一辆摩托车从起点出发沿笔直的赛道向终点行驶,行驶中的速度V(km/h)与时间t(h)的关系部分信息如图所示,根据图象有下列说法:| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
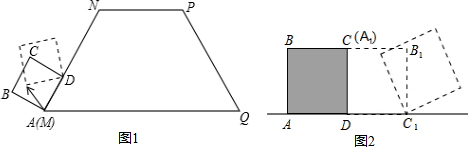
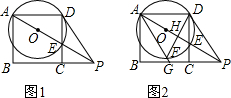 如图1,已知ABCD是边长为4的正方形,E是CD边上的一个动点,连接AE,AE的延长线交BC的延长线于点P,连接PD.作△ADE的外接圆⊙O.设DE=x,PC=y.
如图1,已知ABCD是边长为4的正方形,E是CD边上的一个动点,连接AE,AE的延长线交BC的延长线于点P,连接PD.作△ADE的外接圆⊙O.设DE=x,PC=y. 查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 …
…查看答案和解析>>
科目:初中数学 来源: 题型:解答题
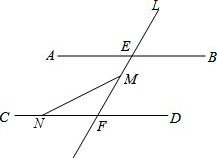 如图,AB∥CD,直L交AB、CD分别于点E、F,点M在线段EF上(点M不与E、F重合),N是直线CD上的一个动点(点N不与F重合)
如图,AB∥CD,直L交AB、CD分别于点E、F,点M在线段EF上(点M不与E、F重合),N是直线CD上的一个动点(点N不与F重合)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com