
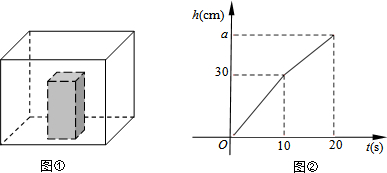
分析 (1)根据图2可知,0~10s时由于实心长方体在水槽里,长方体底面积减小,水面上升的速度较快,所以可知长方体容器中水面恰与实心长方体齐平用了10s,实心长方体的高为30cm;计算出此时水的体积,再除以时间,即可解答;
(2)10~20s时,水淹没实心长方体后一直到水注满,底面积是长方体的底面积,水面上升的速度较慢,所以可知水槽的高度为acm,根据10~20的注水量列出方程,即可解答;
(3)分两种情况求水面高度h(cm)与注水时间t(s)之间的函数关系式;当0<t≤10时,水面高度h与注水时间t的函数图象经过(10,30),
设h=kt,把(10,30)代入,即可解答;当10<t≤20时,水面高度h与注水时间t的函数图象经过(10,30)、(20,50),设h=kt+b,把(10,30)、(20,50)代入,即可解答;当水面高度达到长方体容器高度的一半时,h=25,因为a=30>25,所以25=3t,解得 t=$\frac{25}{3}$.
解答 解:(1)图2可知,0~10s时由于实心长方体在水槽里,长方体底面积减小,水面上升的速度较快,所以可知长方体容器中水面恰与实心长方体齐平用了10s,实心长方体的高为30cm;
∴10s时长方体容器中水的体积为:(60-20)×30=1200cm3,
∴注水速度为:1200÷10=120cm3/s,
故答案为:120.
(2)设长方体容器的高度为acm,
则(a-30)×60=120×10.
∴a=50cm.
∴长方体容器的高为50cm,
(3)当0<t≤10时,水面高度h与注水时间t的函数图象经过(10,30),
设h=kt,把(10,30)代入,得30=10k,
解得:k=3.
∴当0<t≤10时,水面高度h与注水时间t之间的函数关系式为h=3t.
当10<t≤20时,水面高度h与注水时间t的函数图象经过(10,30)、(20,50),
设h=kt+b,
把(10,30)、(20,50)代入,得:$\left\{\begin{array}{l}{30=10k+b}\\{50=20k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=2}\\{b=10}\end{array}\right.$,
∴当10<t≤20时,水面高度h与注水时间t之间的函数关系式为h=2t+10,
当水面高度达到长方体容器高度的一半时,h=25,
∵a=30>25,
∴25=3t,解得t=$\frac{25}{3}$.
∴当水面高度达到长方体容器高度的一半时的t值为$\frac{25}{3}$.
点评 本题主要考查了一次函数的应用以及利用图象获取正确信息,识别函数图象的能力,观察图象提供的信息,再分析高度、时间和容积的关系即可找到解题关键.利用已知图象得出正确信息是考查重点.


科目:初中数学 来源: 题型:解答题
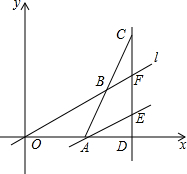 如图,在平面直角坐标系中,点A的坐标为(3,0),直线l与x轴正半轴夹角为30°,点B为直线l上的一个动点,延长AB至点C,使得AB=BC,过点C作CD⊥x轴于点D,交直线l于点F,过点A作AE∥l交直线CD于点E.
如图,在平面直角坐标系中,点A的坐标为(3,0),直线l与x轴正半轴夹角为30°,点B为直线l上的一个动点,延长AB至点C,使得AB=BC,过点C作CD⊥x轴于点D,交直线l于点F,过点A作AE∥l交直线CD于点E.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
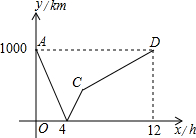 如图所示,一列快车从甲地开往乙地,一列慢车从乙地开往甲地,两车同时出发,设慢车行驶的时间为x小时,两车之间的距离为y千米,图中的折线表示y与x之间的函数关系,则快车的速度是$166\frac{2}{3}$千米/小时.
如图所示,一列快车从甲地开往乙地,一列慢车从乙地开往甲地,两车同时出发,设慢车行驶的时间为x小时,两车之间的距离为y千米,图中的折线表示y与x之间的函数关系,则快车的速度是$166\frac{2}{3}$千米/小时.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
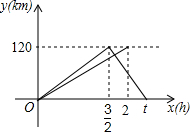 一辆轿车从甲地驶往乙地,到达乙地后立即返回甲地,速度是原来的1.5倍,往返共用t小时;一辆货车同时从甲地驶往乙地,到达乙地后停止,两车同时出发,匀速行驶,设轿车行驶的时间为x(h),两车离开甲地的距离为y(km),两车行驶过程中y与x之间的函数图象如图所示.
一辆轿车从甲地驶往乙地,到达乙地后立即返回甲地,速度是原来的1.5倍,往返共用t小时;一辆货车同时从甲地驶往乙地,到达乙地后停止,两车同时出发,匀速行驶,设轿车行驶的时间为x(h),两车离开甲地的距离为y(km),两车行驶过程中y与x之间的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
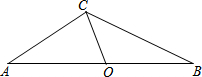 如图,已知钝角三角形ABC,∠A=35°,OC为边AB上的中线,将△AOC绕着点O顺时针旋转,点C落在BC边上的点C′处,点A落在点A′处,联结BA′,如果点A、C、A′在同一直线上,那么∠BA′C′的度数为20°.
如图,已知钝角三角形ABC,∠A=35°,OC为边AB上的中线,将△AOC绕着点O顺时针旋转,点C落在BC边上的点C′处,点A落在点A′处,联结BA′,如果点A、C、A′在同一直线上,那么∠BA′C′的度数为20°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售时段 | A种配餐销售量 | B种配餐销售量 | 销售额 |
| 第一周 | 100份 | 300份 | 5500元 |
| 第二周 | 200份 | 400份 | 8000元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 储水池 | 费用(万元/个) | 可供使用户数(户/个) | 占地面积(m2/个) |
| 新建 | 4 | 5 | 4 |
| 维护 | 3 | 18 | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com