
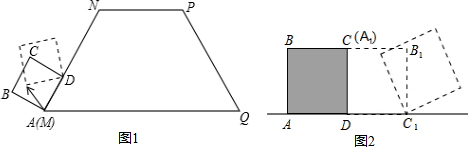
分析 (1)根据点A绕点D翻滚,然后绕点C翻滚,然后绕点B翻滚,半径分别为1、$\sqrt{2}$、1,翻转角分别为90°、90°、150°,据此画出圆弧即可;
(2)根据总结的翻转角度和翻转半径,求出圆弧与梯形的边长围成的扇形的面积即可;
(3)利用正方形纸片ABCD经过4次旋转得出旋转路径,进而得出$\frac{41+20\sqrt{2}}{2}$π=20(1+$\frac{\sqrt{2}}{2}$)π+$\frac{π}{2}$,即可得出旋转次数.
解答 解:(1)作图如图;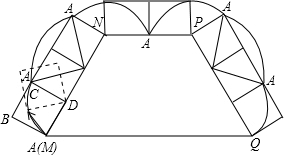
(2)∵点A绕点D翻滚,然后绕点C翻滚,然后绕点B翻滚,半径分别为1、$\sqrt{2}$、1,翻转角分别为90°、90°、150°,
∴S=2×$\frac{90×1×π}{360}$+2×$\frac{90π×(\sqrt{2})^{2}}{360}$+2×$\frac{150π×1}{360}$+4×$\frac{1}{2}$×12
=$\frac{π}{2}$+π+$\frac{5}{6}$π+2
=$\frac{7}{3}$π+2.如图所示.
(3)正方形纸片ABCD经过3次旋转,顶点A在此过程中经过的路程为:
∵$\frac{90×1×π}{180}$×2+$\frac{90π×\sqrt{2}}{180}$=(1+$\frac{\sqrt{2}}{2}$)π,根据第四次正方形旋转时A点不动,也就是此时也是正方形纸片ABCD经过4次旋转的路程;
又$\frac{41+20\sqrt{2}}{2}$π=20(1+$\frac{\sqrt{2}}{2}$)π+$\frac{π}{2}$,
∴正方形纸片OABC经过了:20×4+1=81次旋转.
点评 本题考查了扇形的面积的计算、等腰梯形的性质、弧长的计算,是一道综合了圆的有关计算,旋转的性质的综合题,解题的关键是正确地得到点A的翻转角度和半径.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:解答题
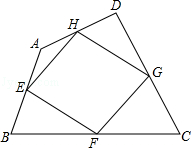 如图,我们把依次连接任意四边形ABCD各边中点所得四边形EFGH叫中点四边形.
如图,我们把依次连接任意四边形ABCD各边中点所得四边形EFGH叫中点四边形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 点的个数 | 可连成直线条数 |
| 2 | l=S2=$\frac{2×1}{2}$ |
| 3 | 3=S3=$\frac{3×2}{2}$ |
| 4 | 6=S4=$\frac{4×3}{2}$ |
| 5 | 10=S5=$\frac{5×4}{2}$ |
| … | … |
| n | Sn=$\frac{n(n-1)}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足$\frac{CF}{FD}$=$\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论:
如图所示,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足$\frac{CF}{FD}$=$\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论:| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
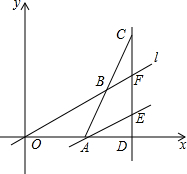 如图,在平面直角坐标系中,点A的坐标为(3,0),直线l与x轴正半轴夹角为30°,点B为直线l上的一个动点,延长AB至点C,使得AB=BC,过点C作CD⊥x轴于点D,交直线l于点F,过点A作AE∥l交直线CD于点E.
如图,在平面直角坐标系中,点A的坐标为(3,0),直线l与x轴正半轴夹角为30°,点B为直线l上的一个动点,延长AB至点C,使得AB=BC,过点C作CD⊥x轴于点D,交直线l于点F,过点A作AE∥l交直线CD于点E.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
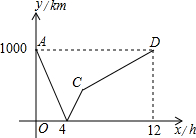 如图所示,一列快车从甲地开往乙地,一列慢车从乙地开往甲地,两车同时出发,设慢车行驶的时间为x小时,两车之间的距离为y千米,图中的折线表示y与x之间的函数关系,则快车的速度是$166\frac{2}{3}$千米/小时.
如图所示,一列快车从甲地开往乙地,一列慢车从乙地开往甲地,两车同时出发,设慢车行驶的时间为x小时,两车之间的距离为y千米,图中的折线表示y与x之间的函数关系,则快车的速度是$166\frac{2}{3}$千米/小时.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com