
| 点的个数 | 可连成直线条数 |
| 2 | l=S2=$\frac{2×1}{2}$ |
| 3 | 3=S3=$\frac{3×2}{2}$ |
| 4 | 6=S4=$\frac{4×3}{2}$ |
| 5 | 10=S5=$\frac{5×4}{2}$ |
| … | … |
| n | Sn=$\frac{n(n-1)}{2}$ |
分析 ①根据平面上有n个点,两点确定一条直线.经过第一个点有n-1条直线,过第二个点B有(n-1)条直线,所以一共可连成n(n-1)条直线,但AB与BA是同一条直线,故应除以2,即Sn=$\frac{n(n-1)}{2}$,由此计算得出答案即可;
②根据表中的计算规律直接得出答案即可;
③根据(2)的结论,代入求得答案即可.
解答 解:①当仅有两个点时,可连成1条直线;当有3个点时,可作出3条直线;当有4个点时,可作出6条直线;当有5个点时,可作出10条直线,当有6点时,可作出$\frac{6×(6-1)}{2}$=15条直线;
②Sn=$\frac{n(n-1)}{2}$;
③当n=2006时,
S2006=$\frac{2006×(2006-1)}{2}$=2011015.
故答案为:15;$\frac{n(n-1)}{2}$;2011015.
点评 此题考查图形的变化规律,观察直线的条数与点的个数之间的关系是解决本题的关键.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 握手图标 | 握手人数 | 握手次数 |
 | 2 | 1 |
 | 3 | 3=1+2 |
 | 4 | 6=1+2+3 |
 | 5 | 10=1+2+3+4 |
| … | … | … |
| … | N | P=1+2+3+…+(n+1) |
| 图标 | 直线条数 | 交点个数 |
 | 2 | 1 |
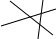 | 3 | 3=1+2 |
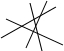 | 4 | |
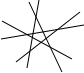 | 5 | |
| … | … | … |
| … | n |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
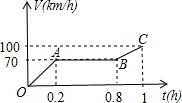 一辆摩托车从起点出发沿笔直的赛道向终点行驶,行驶中的速度V(km/h)与时间t(h)的关系部分信息如图所示,根据图象有下列说法:
一辆摩托车从起点出发沿笔直的赛道向终点行驶,行驶中的速度V(km/h)与时间t(h)的关系部分信息如图所示,根据图象有下列说法:| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 …
…查看答案和解析>>
科目:初中数学 来源: 题型:选择题
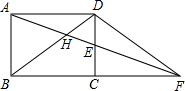 如图,矩形ABCD中,E为CD的中点,连接AE并延长交BC的延长线于点F,连接BD交AF于H,AD=10$\sqrt{2}$,且tan∠EFC=$\frac{\sqrt{2}}{4}$,那么AH的长为( )
如图,矩形ABCD中,E为CD的中点,连接AE并延长交BC的延长线于点F,连接BD交AF于H,AD=10$\sqrt{2}$,且tan∠EFC=$\frac{\sqrt{2}}{4}$,那么AH的长为( )| A. | $\frac{10\sqrt{6}}{3}$ | B. | 5$\sqrt{2}$ | C. | 10 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com