练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    3．计算：$\root{3}{0.001}$-$\sqrt{\frac{1}{100}}$+（-1）3×$\root{2}{（-0.01）^{2}}$．

    分析 根据立方根、平方根、乘方的定义解答．

    解答 解：原式=0.1-$\frac{1}{10}$-1×0.01=-0.01．

    点评 本题考查了实数的运算，熟练掌握立方根、平方根是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

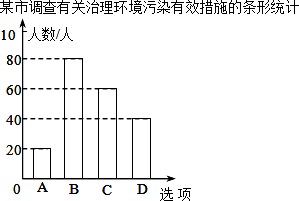    13．某市对市民进行了有关“治理环境污染”的问卷调查，调查问卷内容是“你认为下列哪种治理环境污染的措施最有效？”有以下四个选项（每份调查问卷必答且只选一个选项）：
    （A）植树造林．                      
    （B）控制污水排放．
    （C）禁止城市周边燃烧秸秆．          
    （D）使用清洁能源．
    随机抽取了部分市民进行问卷调查，并将调查结果绘制了如下的条形统计图，请根据图中信息回答下列问题：
    （1）求这次被调查的市民人数．
    （2）求统计图中C所对应的百分比．
    （3）估计该市2 400 000名市民中认同“控制污水排放”的人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

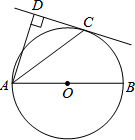    14．如图，AB是⊙O的直径，C是⊙O上一点，AD垂直与过点C的直线，垂足为D，AC平分∠BAD．
    （1）求证：CD是⊙O的切线；
    （2）连接BC，若⊙O的半径为3，BC=2$\sqrt{3}$，求$\frac{AD}{DC}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

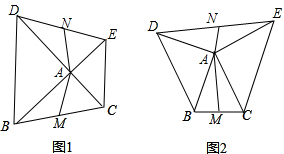
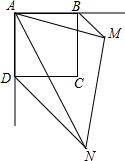    11．已知：如图，正方形ABCD，BM、DN分别是正方形的两个外角平分线，∠MAN=45°，将∠MAN绕着正方形的顶点A旋转，边AM、AN分别交两条角平分线于点M、N，联结MN．
    （1）求证：△ABM∽△NDA；
    （2）联结BD，当∠BAM的度数为多少时，四边形BMND为矩形，并加以证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

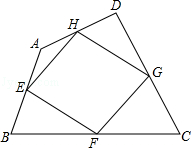    18．如图，我们把依次连接任意四边形ABCD各边中点所得四边形EFGH叫中点四边形．
    （1）若四边形ABCD是菱形，则它的中点四边形EFGH一定是矩形；
    （2）若四边形ABCD的面积为S1，中点四边形EFGH的面积记为S2，则S1与S2的数量关系是S1=2S2；
    （3）在四边形ABCD中，沿中点四边形EFGH的其中三边剪开，可得三个小三角形，将这三个小三角形与原图中未剪开的小三角形拼接成一个平行四边形，请在答题卡的图形上画出一种拼接示意图，并写出对应全等的三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．以△ABC的边AB、AC为直角边分别向外作等腰直角△ABD和△ACE，M是BC的中点，N是DE的中点，连接AM、AN．
    （1）如图1，当∠BAC=90°时，其他条件不变，猜想线段BM与AN之间的数量关系，并证明你的猜想；
    （2）如图2，当∠BAC≠90°时，其他条件不变，那么（1）中猜想的结论是否成立，如果成立，请给出证明；如果不成立，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．如图所示，反比例函数y1=$\frac{6}{x}$的图象与一次函数y2=kx+b的图象交于点A（3，m），B（n，-3），一次函数图象与y轴交于点C．
    （1）求m，n的值；
    （2）直接写出y1＞y2时自变量x的取值范围；
    （3）求△AOC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．以边长为7，24，25的三角形的最大角的顶点为圆心，画一个与最长边相切的圆，则圆的半径长为$\frac{168}{25}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．平面上有n个点（n≥2）且任意三个点不在同一直线上，过这些点中的任两点作直线，一共能作出多少条不同的直线？
    ①分析：当仅有两个点时，可连成1条直线；当有3个点时，可作出3条直线；当有4个点时，可作出6条直线；当有5个点时，可作出10条直线，当有6点时，可作出15条直线．
    ②归纳：考察点的个数n和可作出直线的条数Sn发现如下表所示：Sn=$\frac{n（n-1）}{2}$．
    点的个数可连成直线条数
    2 l=S2=$\frac{2×1}{2}$
    33=S3=$\frac{3×2}{2}$
    4 6=S4=$\frac{4×3}{2}$
    5 10=S5=$\frac{5×4}{2}$
    ……
    n Sn=$\frac{n（n-1）}{2}$
    ③当有2006个点时，可作出直线的条数S2006=2011015．

    查看答案和解析>>

    同步练习册答案