
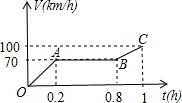
 一辆摩托车从起点出发沿笔直的赛道向终点行驶,行驶中的速度V(km/h)与时间t(h)的关系部分信息如图所示,根据图象有下列说法:
一辆摩托车从起点出发沿笔直的赛道向终点行驶,行驶中的速度V(km/h)与时间t(h)的关系部分信息如图所示,根据图象有下列说法:| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:解答题
 如图所示,反比例函数y1=$\frac{6}{x}$的图象与一次函数y2=kx+b的图象交于点A(3,m),B(n,-3),一次函数图象与y轴交于点C.
如图所示,反比例函数y1=$\frac{6}{x}$的图象与一次函数y2=kx+b的图象交于点A(3,m),B(n,-3),一次函数图象与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 点的个数 | 可连成直线条数 |
| 2 | l=S2=$\frac{2×1}{2}$ |
| 3 | 3=S3=$\frac{3×2}{2}$ |
| 4 | 6=S4=$\frac{4×3}{2}$ |
| 5 | 10=S5=$\frac{5×4}{2}$ |
| … | … |
| n | Sn=$\frac{n(n-1)}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足$\frac{CF}{FD}$=$\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论:
如图所示,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足$\frac{CF}{FD}$=$\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论:| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
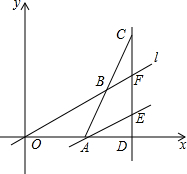 如图,在平面直角坐标系中,点A的坐标为(3,0),直线l与x轴正半轴夹角为30°,点B为直线l上的一个动点,延长AB至点C,使得AB=BC,过点C作CD⊥x轴于点D,交直线l于点F,过点A作AE∥l交直线CD于点E.
如图,在平面直角坐标系中,点A的坐标为(3,0),直线l与x轴正半轴夹角为30°,点B为直线l上的一个动点,延长AB至点C,使得AB=BC,过点C作CD⊥x轴于点D,交直线l于点F,过点A作AE∥l交直线CD于点E.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
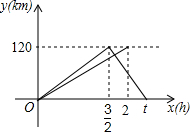 一辆轿车从甲地驶往乙地,到达乙地后立即返回甲地,速度是原来的1.5倍,往返共用t小时;一辆货车同时从甲地驶往乙地,到达乙地后停止,两车同时出发,匀速行驶,设轿车行驶的时间为x(h),两车离开甲地的距离为y(km),两车行驶过程中y与x之间的函数图象如图所示.
一辆轿车从甲地驶往乙地,到达乙地后立即返回甲地,速度是原来的1.5倍,往返共用t小时;一辆货车同时从甲地驶往乙地,到达乙地后停止,两车同时出发,匀速行驶,设轿车行驶的时间为x(h),两车离开甲地的距离为y(km),两车行驶过程中y与x之间的函数图象如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com