
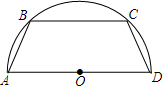
 如图,四边形ABCD内接于半圆,AB=CD,BC∥AD,且AB=1,BC=2,则OA为$\frac{1+\sqrt{3}}{2}$.
如图,四边形ABCD内接于半圆,AB=CD,BC∥AD,且AB=1,BC=2,则OA为$\frac{1+\sqrt{3}}{2}$. 分析 根据题意利用勾股定理表示出BE,OG的长,进而结合一元二次方程的解法得出即可.
解答 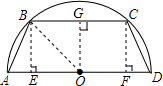 解:分别过点B、点C作BE⊥AD于点E,CF⊥AD于点F,再过点O作OG⊥BC于点G,连接OB,
解:分别过点B、点C作BE⊥AD于点E,CF⊥AD于点F,再过点O作OG⊥BC于点G,连接OB,
因为四边形ABCD是等腰梯形,AB=1,BC=2,
则BE=OG=CF,BG=GC=EO=OF=$\frac{1}{2}$EF=$\frac{1}{2}$BC=1,AB=CD=1,
设OA=OD=OB=x,
则AE=x-1,
所以BE=$\sqrt{A{B}^{2}-A{E}^{2}}$=$\sqrt{1-(x-1)^{2}}$=$\sqrt{2x-{x}^{2}}$,
又因为OG=$\sqrt{O{B}^{2}-B{G}^{2}}$=$\sqrt{{x}^{2}-1}$,
又因为OG=BE,
所以$\sqrt{2x-{x}^{2}}$=$\sqrt{{x}^{2}-1}$,
所以2x-x2=x2-1,
则2x2-2x-1=0,
解得:x=$\frac{1+\sqrt{3}}{2}$或$\frac{1-\sqrt{3}}{2}$(舍去),
即OA=$\frac{1+\sqrt{3}}{2}$.
故答案为:$\frac{1+\sqrt{3}}{2}$.
点评 此题主要考查了勾股定理以及垂径定理和一元二次方程的解法,表示出BE,GO的长是解题关键.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com