
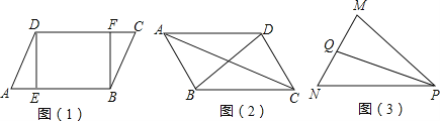
【题目】(1)如图(1),在平行四边形ABCD中,DE⊥AB,BF⊥CD,垂足分别为E、F,求证:AE=CF;
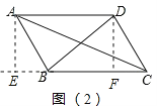
(2)如图(2),在平行四边形ABCD中,AC、BD是两条对角线,求证AC2+BD2=2(AB2+BC2)
(3)如图(3),PQ是△PMN的中线,若PM=11,PN=13,MN=10,求出PQ的长度.
【答案】(1)见解析;(2)见解析;(3)2![]()
【解析】
(1)利用平行四边形的性质,判定Rt△AED≌Rt△CFB,即可得到AE=CF;
(2)分别过A,D作AE⊥BC交CB延长线于E,DF⊥BC于F.根据勾股定理可得:AC2=AE2+(BE+BC)2①,AE2=AB2-BE2②,BD2=DF2+(BC-CF)2③,DF2=DC2-CF2④,②代①,④代③,两式相加即可得到结论;
(3)延长PQ至R,使得QR=PQ,连接RM,RN,依据四边形NPMR是平行四边形,利用结论MN2+PR2=2(NP2+MP2),即可得出PQ的长.
解:(1)∵平行四边形ABCD中,DE⊥AB,BF⊥CD,
∴AD=CB,DE=BF,∠AED=∠CFB=90°,
在Rt△AED≌Rt△CFB中,
![]() ,
,
∴Rt△AED≌Rt△CFB(HL),
∴AE=CF;
(2)如图(2),分别过A,D作AE⊥BC交CB延长线于E,DF⊥BC于F.
根据勾股定理可得:AC2=AE2+(BE+BC )2 ①,AE2=AB2-BE2②,
BD2=DF2 +(BC-CF)2 ③,DF2=DC2-CF2 ④,
∵四边形ABCD是平行四边形,
∴AB=DC,
又∵AE⊥BC,DF⊥BC,
∴∠AEB=∠DFC=90°,AE=DF,
∴Rt△AEB≌Rt△DFC(HL),
∴BE=CF,而AB=DC,
把②代①,④代③,可得:
AC2=AB2 -BE2 +(BE+BC)2
BD2=DC2 -CF2+(BC-CF)2
两式相加,可得:AC2 +BD2=2(AB2 +BC2);
(3)如图(3),延长PQ至R,使得QR=PQ,连接RM,RN,
∵PQ是△PMN的中线,
∴NQ=MQ,
∴四边形NPMR是平行四边形,
由(2)可得,MN2 +PR2=2(NP2 +MP2),
又∵PM=11,PN=13,MN=10,
∴102 +(2PQ)2=2(132+112),
解得PQ=2![]() .
.


科目:初中数学 来源: 题型:
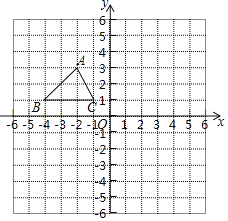
【题目】△ABC在直角坐标系中的位置如图,其中A点的坐标是(﹣2,3)
(1)△ABC绕点O顺时针旋转90°得到△A1B1C1,请作出△A1B1C1,并写出A点的对应点A1的坐标;
(2)若△ABC经过平移后A点的对应点A2的坐标是(2,﹣1),请作△A2B2C2,并计算平移的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,AB=3,BC=4,AC=5,在直线BC上有P点,使△PAC是以AC为腰的等腰三角形,则BP的长为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 为
为![]() 边上的中点.
边上的中点.
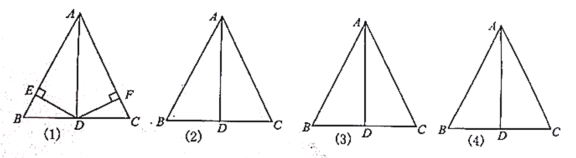
(1)若![]() 于
于![]() ,
,![]() 于
于![]() ,连接
,连接![]() .判断
.判断![]() 的形状,并证明;
的形状,并证明;
(2)若![]() 分别是
分别是![]() 上的中线,连接
上的中线,连接![]() .判断
.判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)若![]() 分别是
分别是![]() 的平分线,连接
的平分线,连接![]() .判断
.判断![]() 的关系,不需证明;
的关系,不需证明;
(4)若分别在![]() 上任取一点
上任取一点![]() ,且
,且![]() ,连接
,连接![]() .在不添加辅助线的情况下,你还能得到哪些不同于上面的正确结论?请写出至少四条,不需证明.
.在不添加辅助线的情况下,你还能得到哪些不同于上面的正确结论?请写出至少四条,不需证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
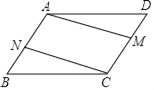
【题目】如图,在四边形ABCD中,AB∥CD,AD∥BC,AN=CM.
(1)求证:BN=DM;
(2)若BC=3,CD=2,∠B=50°,求∠BCD、∠D的度数及四边形ABCD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在进行二次根式化简时,我们有时会碰上如![]() ,
,![]() ,
,![]() 一样的式子,这样的式子我们可以将其进一步化简
一样的式子,这样的式子我们可以将其进一步化简![]() =
=![]() ,
,![]() ,
,![]() 以上这种化简的方法叫做分母有理化,请利用分母有理化解答下列问题:
以上这种化简的方法叫做分母有理化,请利用分母有理化解答下列问题:
(1)化简:![]() ;
;
(2)若a是![]() 的小数部分,求
的小数部分,求![]() 的值;
的值;
(3)矩形的面积为3![]() +1,一边长为
+1,一边长为![]() ﹣2,求它的周长.
﹣2,求它的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
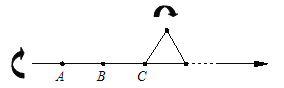
【题目】将数轴按如图所示从某一点开始折出一个等边![]() ,设点
,设点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() ,若将
,若将![]() 向右滚动,则
向右滚动,则![]() 的值等于_____;数字
的值等于_____;数字![]() 对应的点将与
对应的点将与![]() 的顶点______重合.
的顶点______重合.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径作⊙O,点D为⊙O上一点,且CD=CB、连接DO并延长交CB的延长线于点E.
(1)判断直线CD与⊙O的位置关系,并说明理由;
(2)若BE=4,DE=8,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于D,交AB于E,F在DE上,且AF∥CE.
(1)说明四边形ACEF是平行四边形;(2)当∠B满足什么条件时,四边形ACEF是菱形,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com