
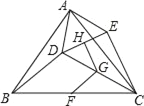
【题目】如图,△ABC为等腰三角形,AB=AC,D为△ABC内一点,连接AD,将线段AD绕点A旋转至AE,使得∠DAE=∠BAC,F,G,H分别为BC,CD,DE的中点,连接BD,CE,GF,GH.
(1)求证:GH=GF;
(2)试说明∠FGH与∠BAC互补.
【答案】(1)证明见解析;(2)说明见解析.
【解析】
(1)首先得出△ABD≌△ACE(SAS),进而利用三角形中位线定理得出GH=GF;
(2)利用全等三角形的性质结合平行线的性质得出∠FGH=∠DGF+∠HGD进而得出答案.
(1)∵∠DAE=∠BAC,
∴∠BAD=∠CAE,
在△ABD和△ACE中
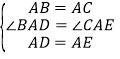 ,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,
∵F,G,H分别为BC,CD,DE的中点,
∴HG∥CE,GF∥BD,且GH=![]() CE,GF=
CE,GF=![]() BD,
BD,
∴GH=GF;
(2)∵△ABD≌△ACE,
∴∠ABD=∠ACE,
∵HG∥CE,GF∥BD,
∴∠HGD=∠ECD,∠GFC=∠DBC,
∴∠HGD=∠ACD+∠ECA=∠ACD+∠ABD,
∠DGF=∠GFC+∠GCF=∠DBC+∠GCF,
∴∠FGH=∠DGF+∠HGD
=∠DBC+∠GCF+∠ACD+∠ABD
=∠ABC+∠ACB
=180°﹣∠BAC,
∴∠FGH与∠BAC互补.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:
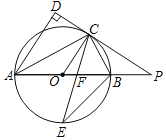
【题目】如图,已知AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.
(1)求证:AC平分∠DAB;
(2)求证:△PCF是等腰三角形;
(3)若AF=6,EF=2![]() ,求⊙O的半径长.
,求⊙O的半径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
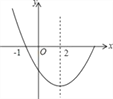
【题目】如图,是抛物线y=ax2+bx+c(a≠0)图象的一部分,已知抛物线的对称轴为x=2,与x轴的一个交点是(﹣1,0).下列结论:
①ac<0;②4a﹣2b+c>0;③抛物线与x轴的另一个交点是(4,0);
④点(﹣3,y1),(6,y2)都在抛物线上,则有y1<y2.其中正确的个数为( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大学生创业团队抓住商机,购进一批干果分装成营养搭配合理的小包装后出售,每袋成本3元.试销期间发现每天的销售量y(袋)与销售单价x(元)之间满足一次函数关系,部分数据如表所示,其中3.5≤x≤5.5,另外每天还需支付其他各项费用80元.
销售单价x(元) | 3.5 | 5.5 |
销售量y(袋) | 280 | 120 |
(1)请直接写出y与x之间的函数关系式;
(2)如果每天获得160元的利润,销售单价为多少元?
(3)设每天的利润为w元,当销售单价定为多少元时,每天的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
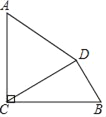
【题目】如图,已知AC⊥BC,垂足为C,AC=4,BC=3![]() ,将线段AC绕点A按逆时针方向旋转60°,得到线段AD,连接DC,DB.
,将线段AC绕点A按逆时针方向旋转60°,得到线段AD,连接DC,DB.
(1)求线段CD的长;
(2)求线段DB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在北海市创建全国文明城活动中,需要30名志愿者担任“讲文明树新风”公益广告宣传工作,其中男生18人,女生12人.
(1)若从这30人中随机选取一人作为“展板挂图”讲解员,求选到女生的概率;
(2)若“广告策划”只在甲、乙两人中选一人,他们准备以游戏的方式决定由谁担任,游戏规则如下:将四张牌面数字分别为2,3,4,5的扑克牌洗匀后,数字朝下放于桌面,从中任取2张,若牌面数字之和为偶数,则甲担任,否则乙担任.试问这个游戏公平吗?请用树状图或列表法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
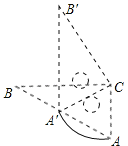
【题目】如图,△ABC和△A′B′C是两个完全重合的直角三角板,∠B=30°,斜边长为10cm.三角板A′B′C绕直角顶点C顺时针旋转,当点A′落在AB边上时,CA′旋转所构成的扇形的弧长为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
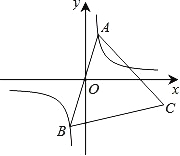
【题目】如图,已知点A是双曲线![]() 在第一象限分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第四象限内,且随着点A的运动,点C的位置也在不断变化,但点C始终在双曲线
在第一象限分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第四象限内,且随着点A的运动,点C的位置也在不断变化,但点C始终在双曲线![]() 上运动,则k的值是 .
上运动,则k的值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解下列方程,其中应在方程左右两边同时加上4的是( )
A. x2﹣2x=5 B. x2+4x=5 C. 2x2﹣4x=5 D. 4x2+4x=5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com