
【题目】如图,已知点A是双曲线![]() 在第一象限分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第四象限内,且随着点A的运动,点C的位置也在不断变化,但点C始终在双曲线
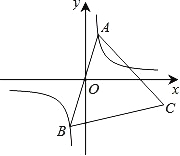
在第一象限分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第四象限内,且随着点A的运动,点C的位置也在不断变化,但点C始终在双曲线![]() 上运动,则k的值是 .
上运动,则k的值是 .
【答案】﹣3![]()
【解析】
试题根据反比例函数的性质得出OA=OB,连接OC,过点A作AE⊥y轴,垂足为E,过点C作CF⊥y轴,垂足为F,根据等边三角形的性质和解直角三角形求出OC=![]() OA,求出△OFC∽△AEO,相似比
OA,求出△OFC∽△AEO,相似比![]() ,求出面积比
,求出面积比 ,求出△OFC的面积,即可得出答案.∵双曲线
,求出△OFC的面积,即可得出答案.∵双曲线![]() 的图象关于原点对称,
的图象关于原点对称,
∴点A与点B关于原点对称, ∴OA=OB, 连接OC,如图所示, ∵△ABC是等边三角形,OA=OB,
∴OC⊥AB.∠BAC=60°, ∴tan∠OAC=![]() =
=![]() , ∴OC=
, ∴OC=![]() OA,
OA,
过点A作AE⊥y轴,垂足为E,过点C作CF⊥y轴,垂足为F, ∵AE⊥OE,CF⊥OF,OC⊥OA,
∴∠AEO=∠OFC,∠AOE=90°﹣∠FOC=∠OCF, ∴△OFC∽△AEO,相似比![]() , ∴面积比
, ∴面积比 ,
,
∵点A在第一象限,设点A坐标为(a,b), ∵点A在双曲线![]() 上, ∴S△AEO=
上, ∴S△AEO=![]() ab=
ab=![]() ,
,
∴S△OFC=![]() FCOF=
FCOF=![]() , ∴设点C坐标为(x,y), ∵点C在双曲线
, ∴设点C坐标为(x,y), ∵点C在双曲线![]() 上, ∴k=xy,
上, ∴k=xy,
∵点C在第四象限, ∴FC=x,OF=﹣y. ∴FCOF=x(﹣y)=﹣xy=﹣![]()



 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
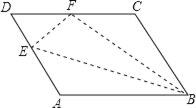
【题目】如图,平行四边形ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在边CD上的点F处,若△DEF的周长为8,△CBF的周长为18,则FC的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
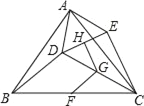
【题目】如图,△ABC为等腰三角形,AB=AC,D为△ABC内一点,连接AD,将线段AD绕点A旋转至AE,使得∠DAE=∠BAC,F,G,H分别为BC,CD,DE的中点,连接BD,CE,GF,GH.
(1)求证:GH=GF;
(2)试说明∠FGH与∠BAC互补.
查看答案和解析>>
科目:初中数学 来源: 题型:
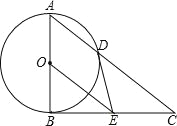
【题目】如图,在△ABC中,∠ABC=90°,以AB的中点O为圆心、OA为半径的圆交AC于点D,E是BC的中点,连接DE,OE.
(1)判断DE与⊙O的位置关系,并说明理由;
(2)求证:BC2=2CD·OE;
(3)若cos∠BAD=![]() ,BE=6,求OE的长.
,BE=6,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
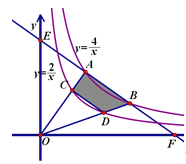
【题目】已知,如图双曲线![]() (x>0)与直线EF交于点A,点B,且AE=AB=BF,连结AO,BO,它们分别与双曲线
(x>0)与直线EF交于点A,点B,且AE=AB=BF,连结AO,BO,它们分别与双曲线![]() (x>0)交于点C,点D,则:
(x>0)交于点C,点D,则:
(1)AB与CD的位置关系是__________;
(2)四边形ABDC的面积为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,已知O是坐标原点,B、C两点的坐标分别为(3,-1)、(2,1)。

(1)以O点为位似中心在y轴的左侧将△OBC放大到两倍画出图形。
(2)写出B、C两点的对应点B、C的坐标;
(3)如果△OBC内部一点M的坐标为(x,y),写出M的对应点M的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有红、白两种颜色的小球,这些球除颜色外完全相同,其中红球有![]() 个,若从中随机摸出一个球,这个球是白球的概率为
个,若从中随机摸出一个球,这个球是白球的概率为![]() .
.
(![]() )请直接写出袋子中白球的个数.
)请直接写出袋子中白球的个数.
(![]() )随机摸出一个球后,放回并搅匀,再随机摸出一个球,求两次都摸到相同颜色的小球的概率.(请结合树状图或列表解答)
)随机摸出一个球后,放回并搅匀,再随机摸出一个球,求两次都摸到相同颜色的小球的概率.(请结合树状图或列表解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形 OABC 是矩形,点 B 的坐标为(4,3).
(1)直接写出A、C两点的坐标;
(2)平行于对角线AC的直线 m 从原点O出发,沿 x 轴正方向以每秒 1 个单位长度的速度运动,设直线 m 与矩形 OABC 的两边分别交于点M、N,设直线m运动的时间为t(秒).
①若 MN=![]() AC,求 t 的值;
AC,求 t 的值;
②设△OMN 的面积为S,当 t 为何值时,S=![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com