
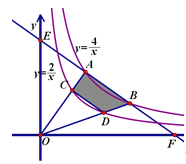
【题目】已知,如图双曲线![]() (x>0)与直线EF交于点A,点B,且AE=AB=BF,连结AO,BO,它们分别与双曲线
(x>0)与直线EF交于点A,点B,且AE=AB=BF,连结AO,BO,它们分别与双曲线![]() (x>0)交于点C,点D,则:
(x>0)交于点C,点D,则:
(1)AB与CD的位置关系是__________;
(2)四边形ABDC的面积为__________.
【答案】(1)AB∥CD;(2)![]() .
.
【解析】
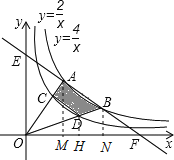
如图,过点A作AM⊥x轴于点M,过点D作DH⊥x轴于点H,过点B作BN⊥x轴于点N,即可得AM∥DH∥BN∥y轴,设点A的坐标为(m,![]() ),由AE=AB=BF,可得OM=MN=BN,所以点B的坐标为(2m,
),由AE=AB=BF,可得OM=MN=BN,所以点B的坐标为(2m,![]() ),所以S△OAB=S△OAM+S梯形AMNB-S△OBN=2+
),所以S△OAB=S△OAM+S梯形AMNB-S△OBN=2+![]() ×(
×(![]() +
+![]() )×(2m-m)-2=3,因为DH∥BN,可得△ODH∽△OBN,根据相似三角形的性质可得
)×(2m-m)-2=3,因为DH∥BN,可得△ODH∽△OBN,根据相似三角形的性质可得![]() ,根据反比例函数k的几何意义可得DHOH=2,BNON=4,所以(
,根据反比例函数k的几何意义可得DHOH=2,BNON=4,所以(![]() )2=
)2=![]() =
=![]() ,同理可得(
,同理可得(![]() )2=
)2=![]() ,即
,即![]() =
=![]() ,所以AB∥CD ;由
,所以AB∥CD ;由![]() =
=![]() ,∠COD=∠AOB,可得△COD∽△AOB,由相似三角形的性质可得
,∠COD=∠AOB,可得△COD∽△AOB,由相似三角形的性质可得![]() ,所以S△COD=
,所以S△COD=![]() ,即可得S四边形ABDC=
,即可得S四边形ABDC=![]() .
.


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:
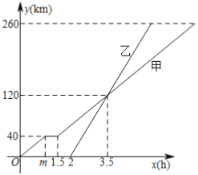
【题目】已知甲、乙两车分别以各自的速度匀速从![]() 地驶向
地驶向![]() 地,甲车比乙车早出发
地,甲车比乙车早出发![]() ,并且甲车途中休息了
,并且甲车途中休息了![]() ,如图是甲、乙两车行驶的路程
,如图是甲、乙两车行驶的路程![]() 与时间
与时间![]() 的函数图象.
的函数图象.
(1)求图中![]() 的值及
的值及![]() 、
、![]() 两地的距离;
两地的距离;
(2)求出甲车行驶路程![]() 与时间
与时间![]() 的函数解析式,并写出相应的
的函数解析式,并写出相应的![]() 的取值范围;
的取值范围;
(3)小明说:乙车行驶路程![]() 与时间
与时间![]() 的函数解析式为
的函数解析式为![]() .问:①小明的说法对吗?简要说明理由;②当乙车行驶多长时间时,两车恰好相距
.问:①小明的说法对吗?简要说明理由;②当乙车行驶多长时间时,两车恰好相距![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
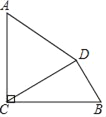
【题目】如图,已知AC⊥BC,垂足为C,AC=4,BC=3![]() ,将线段AC绕点A按逆时针方向旋转60°,得到线段AD,连接DC,DB.
,将线段AC绕点A按逆时针方向旋转60°,得到线段AD,连接DC,DB.
(1)求线段CD的长;
(2)求线段DB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
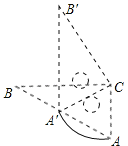
【题目】如图,△ABC和△A′B′C是两个完全重合的直角三角板,∠B=30°,斜边长为10cm.三角板A′B′C绕直角顶点C顺时针旋转,当点A′落在AB边上时,CA′旋转所构成的扇形的弧长为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角三角形的直角顶点在坐标原点,∠OAB=30°,若点A在反比例函数y=![]() (x>0)的图象上,则经过点B的反比例函数解析式为( )
(x>0)的图象上,则经过点B的反比例函数解析式为( )

A. y=﹣![]() B. y=﹣
B. y=﹣![]() C. y=﹣
C. y=﹣![]() D. y=
D. y=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
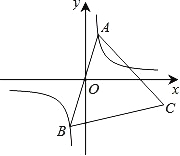
【题目】如图,已知点A是双曲线![]() 在第一象限分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第四象限内,且随着点A的运动,点C的位置也在不断变化,但点C始终在双曲线
在第一象限分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第四象限内,且随着点A的运动,点C的位置也在不断变化,但点C始终在双曲线![]() 上运动,则k的值是 .
上运动,则k的值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
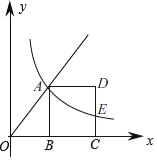
【题目】如图,点A是射线y=![]() (x≥0)上一点,过点A作AB⊥x轴于点B,以AB为边在其右侧作正方形ABCD,过点A的双曲线y=
(x≥0)上一点,过点A作AB⊥x轴于点B,以AB为边在其右侧作正方形ABCD,过点A的双曲线y=![]() 交CD边于点E,则
交CD边于点E,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.1
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
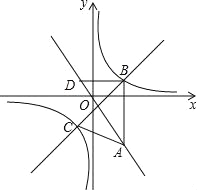
【题目】如图,在平面直角坐标系xOy中,点A(a,﹣![]() )在直线y=﹣
)在直线y=﹣![]() 上,AB∥y轴,且点B的纵坐标为1,双曲线y=
上,AB∥y轴,且点B的纵坐标为1,双曲线y=![]() 经过点B.
经过点B.
(1)求a的值及双曲线y=![]() 的解析式;
的解析式;
(2)经过点B的直线与双曲线y=![]() 的另一个交点为点C,且△ABC的面积为
的另一个交点为点C,且△ABC的面积为![]() .
.
①求直线BC的解析式;
②过点B作BD∥x轴交直线y=﹣![]() 于点D,点P是直线BC上的一个动点.若将△BDP以它的一边为对称轴进行翻折,翻折前后的两个三角形所组成的四边形为正方形,直接写出所有满足条件的点P的坐标.
于点D,点P是直线BC上的一个动点.若将△BDP以它的一边为对称轴进行翻折,翻折前后的两个三角形所组成的四边形为正方形,直接写出所有满足条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一儿童服装商店在销售中发现:某品牌童装平均每天可售出20件,每件盈利40元.为了迎接“六·一”儿童节,商店决定采取适当的降价措施,扩大销售量,增加盈利,尽快减少库存.经市场调查发现:如果每件童装降价1元,那么平均每天就可多售出2件.要想平均每天销售这种童装上盈利1200元,那么每件童装应降价多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com