
����Ŀ����֪�ס��������ֱ��Ը��Ե��ٶ����ٴ�![]() ��ʻ��
��ʻ��![]() �أ��׳����ҳ������
�أ��׳����ҳ������![]() �����Ҽ׳�;����Ϣ��
�����Ҽ׳�;����Ϣ��![]() ����ͼ�Ǽס���������ʻ��·��
����ͼ�Ǽס���������ʻ��·��![]() ��ʱ��
��ʱ��![]() �ĺ���ͼ��
�ĺ���ͼ��
��1����ͼ��![]() ��ֵ��
��ֵ��![]() ��
��![]() ���صľ��룻
���صľ��룻
��2������׳���ʻ·��![]() ��ʱ��
��ʱ��![]() �ĺ�������ʽ����д����Ӧ��
�ĺ�������ʽ����д����Ӧ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3��С��˵���ҳ���ʻ·��![]() ��ʱ��
��ʱ��![]() �ĺ�������ʽΪ
�ĺ�������ʽΪ![]() ���ʣ���С����˵�����𣿼�Ҫ˵�����ɣ��ڵ��ҳ���ʻ�ʱ��ʱ������ǡ�����
���ʣ���С����˵�����𣿼�Ҫ˵�����ɣ��ڵ��ҳ���ʻ�ʱ��ʱ������ǡ�����![]() ��
��
���𰸡���1��1��260����2��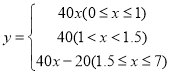 ����3����С����˵���ǶԵģ����ɼ���������
����3����С����˵���ǶԵģ����ɼ���������![]() Сʱ��
Сʱ��![]() Сʱ
Сʱ
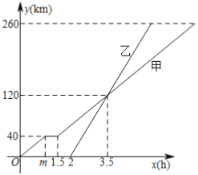
��������
(1)���ݼ׳�;����Ϣ��0��5h�������m��ֵ���ٸ���ͼ����ü׳����ٶȣ����ɵõ�a����ͼ���֪A��B����֮����룮
(2)��������ͺ���ͼ���ĵ㼴������Ա���x�ڲ�ͬȡֵ��Χ�ڵĺ�����ϵʽ��
(3)���ݺ����ϵĵ����������ҳ���ʻ��·��y��ʱ��x�ĺ�����ϵʽ���ٸ���·�����50km��÷���������xֵ�������������������ҳ���ʻʱ�䣮
��1���������֪�׳�;����Ϣ��![]() �����ݼ׳��ĺ���ͼ���֪·��y��������伴Ϊ����;��Ϣ��ʱ�䣬
�����ݼ׳��ĺ���ͼ���֪·��y��������伴Ϊ����;��Ϣ��ʱ�䣬
1.5m=0.5
m=1
�ɺ���ͼ���֪A��B����֮�����Ϊ260km��
�ʴ𰸣�1��260
��2����![]() ʱ����y��x֮��ĺ�����ϵʽΪy=k1x�������⣬��
ʱ����y��x֮��ĺ�����ϵʽΪy=k1x�������⣬��
k1=40
��y=40x(![]() )
)
��![]() ʱ��y=40(
ʱ��y=40(![]() )��
)��
��![]() ����y��x֮��ĺ�����ϵʽΪy=k2x+b��
����y��x֮��ĺ�����ϵʽΪy=k2x+b��
�ߴ�ʱ����ͼ����(1.5��40)��(3.5��120)
��
��ã�k2=40��b=-20
��y=40x-20
��y=260ʱ��x=7����x��ȡֵ��ΧΪ![]()
��������
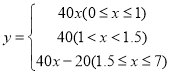
��3�������ҳ���ʻ��·��y��ʱ��x֮��Ľ���ʽΪy=k3x+b3��ͼ����(2��0)��(3.5��120)��
��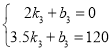
��ã�k3=80��b3=-160
��y=80x160
��֪��С����˵���ǶԵģ�
�ڵ�һ����������ҳ���ʻxСʱ�����׳���ǰʱ���������![]()
��40x20(80x-160)=50
��ã�x=![]() ��
��![]() -2=
-2=![]()
�ڶ���������׳��ں�ʱ����
80x-160-(40x-20)=50
��ã�x=![]() ��
��![]() 2=
2=![]()
���ҳ���ʻ![]() Сʱ��
Сʱ��![]() Сʱ������ǡ�����50km��
Сʱ������ǡ�����50km��


 ���źþ���Ԫ����ĩ��ϵ�д�
���źþ���Ԫ����ĩ��ϵ�д� һ����ʦȨ����ҵ��ϵ�д�
һ����ʦȨ����ҵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y=x2+bx+c��x�ύ��A��B����A�ڵ�B����ࣩ����y�ύ�ڵ�C��0����3�����Գ�����ֱ��x=1��ֱ��BC�������ߵĶԳ��ύ�ڵ�D��
��1���������ߵĺ�������ʽ��
��2����ֱ��BC�ĺ�������ʽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���ACB=90������B,C����ġ�O��AC�ڵ�D����AB�ڵ�E������EO���ӳ�����O�ڵ�F.����BF,CF.����EDC=135��,CF=![]() ,��AE2+BE2��ֵΪ �� ��
,��AE2+BE2��ֵΪ �� ��

A. 8 B. 12 C. 16 D. 20
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��������һ��ˮ�����ż�Ϊÿ��40Ԫ���涨�ۼ۲����ڽ��ۣ����ڵ��ۼ�Ϊÿ��72Ԫ��ÿ�¿�����60�䣮���г����鷢�֣�������ţ�̵��ۼ�ÿ����2Ԫ����ÿ�µ�����������10�䣬��ÿ��ˮ������xԪ��xΪż������ÿ�µ�����Ϊy�䣮
(1)д��y��x֮��ĺ�����ϵʽ���Ա���x��ȡֵ��Χ��
(2)���ó��������۹�����ÿ����֧����������500Ԫ������ζ��۲���ʹÿ������ˮ�������������������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y��ax2��bx��c��a��0�����ú���y���Ա���x�IJ��ֶ�Ӧֵ���±���
x | �� | 1 | 2 | 3 | �� |
y | �� | 0 | ��1 | 0 | �� |
(1)��ö��κ����ı���ʽ��
(2)����ʽax2��bx��c��0�Ľ⼯Ϊ ��
����ʽax2��bx��c��3�Ľ⼯Ϊ .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
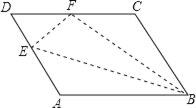
����Ŀ����ͼ��ƽ���ı���ABCD�У���E�ڱ�AD�ϣ���BEΪ�ۺۣ�����ABE���Ϸ��ۣ���A�������ڱ�CD�ϵĵ�F��������DEF���ܳ�Ϊ8����CBF���ܳ�Ϊ18����FC�ij�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
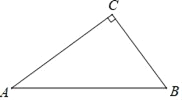
����Ŀ����ͼ���ڡ�ABC�У���ACB��90�㣮
��1������������B��Բ��O��б��AB�������AC�����ڵ�E�ġ�O��Ҫ���ó߹���ͼ��������ͼ�ۼ�����д������֤����
��2���裨1���������ġ�O���AB�������ڵ�B������һ��D������O��ֱ��Ϊ5��BC��4����DE�ij���������ó߹���ͼ������ͼ�Σ��ɻ�����ͼ��ɣ�2���ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����������ţ���������ˮ��2mʱ��ˮ���4m��ˮ���½�2m��ˮ���������______m.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
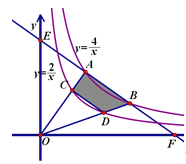
����Ŀ����֪����ͼ˫����![]() ��x>0)��ֱ��EF���ڵ�A����B����AE=AB=BF������AO��BO�����Ƿֱ���˫����
��x>0)��ֱ��EF���ڵ�A����B����AE=AB=BF������AO��BO�����Ƿֱ���˫����![]() ��x>0)���ڵ�C����D����
��x>0)���ڵ�C����D����
��1��AB��CD��λ�ù�ϵ��__________��
��2���ı���ABDC�����Ϊ__________��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com