
【题目】某宾馆有客房![]() 间供游客居住,当每间客房的定价为每天
间供游客居住,当每间客房的定价为每天![]() 元时,客房恰好全部住满;如果每间客房每天的定价每增加
元时,客房恰好全部住满;如果每间客房每天的定价每增加![]() 元,就会减少
元,就会减少![]() 间客房出租.设每间客房每天的定价增加
间客房出租.设每间客房每天的定价增加![]() 元,宾馆出租的客房为
元,宾馆出租的客房为![]() 间.求:
间.求:
![]() 关于
关于![]() 的函数关系式;
的函数关系式;
![]() 如果某天宾馆客房收入
如果某天宾馆客房收入![]() 元,那么这天每间客房的价格是多少元?
元,那么这天每间客房的价格是多少元?
【答案】(1)y=-![]() x+200;(2)这天的每间客房的价格是
x+200;(2)这天的每间客房的价格是![]() 元或
元或![]() 元.
元.
【解析】
(1)根据题意直接写出函数关系式,然后整理即可;
(2)用每间房的收入(180+x),乘以出租的房间数(-![]() x+200)等于总收入列出方程求解即可.
x+200)等于总收入列出方程求解即可.
(1)设每间客房每天的定价增加x元,宾馆出租的客房为y间,
根据题意,得:y=200-4×![]() ,
,
∴y=-![]() x+200;
x+200;
(2)设每间客房每天的定价增加x元,
根据题意,得(180+x)(-![]() x+200)=38400,
x+200)=38400,
整理后,得x2-320x+6000=0,
解得x1=20,x2=300,
当x=20时,x+180=200(元),
当x=300时,x+180=480(元),
答:这天的每间客房的价格是200元或480元.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,已知AD∥BC,点E是CD上一点,AE平分∠BAD,BF平分∠ABC,延长BE交AD的延长线于点F
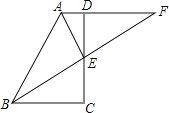
(1)求证:△ABE≌△AFE;
(2)若AD=2,BC=6,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 与x、y轴分别交于A、B两点,
与x、y轴分别交于A、B两点,![]() 与x、y轴交于C、D两点.
与x、y轴交于C、D两点.
(1)求A、B、C、D的坐标(用含k、m的代数式表示);
(2)若![]() ,求
,求![]() 的值;
的值;
(3)在(2)的前提下,若![]() 的面积为27,求m的值.
的面积为27,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() .
.
![]() 当抛物线的顶点在
当抛物线的顶点在![]() 轴上时,求该抛物线的解析式;
轴上时,求该抛物线的解析式;
![]() 不论
不论![]() 取何值时,抛物线的顶点始终在一条直线上,求该直线的解析式;
取何值时,抛物线的顶点始终在一条直线上,求该直线的解析式;
![]() 若有两点
若有两点![]() ,且该抛物线与线段
,且该抛物线与线段![]() 始终有交点,请直接写出
始终有交点,请直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=![]() x与双曲线y=
x与双曲线y=![]() 交于A、B两点,且点A的横坐标为
交于A、B两点,且点A的横坐标为![]() .
.
(1)求k的值;
(2)若双曲线y=![]() 上点C的纵坐标为3,求△AOC的面积;
上点C的纵坐标为3,求△AOC的面积;
(3)在坐标轴上有一点M,在直线AB上有一点P,在双曲线y=![]() 上有一点N,若以O、M、P、N为顶点的四边形是有一组对角为60°的菱形,请写出所有满足条件的点P的坐标.
上有一点N,若以O、M、P、N为顶点的四边形是有一组对角为60°的菱形,请写出所有满足条件的点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=6,BC=8.
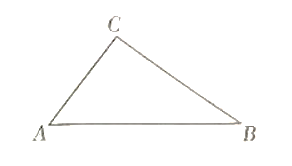
(1)用直尺和圆规作∠A的平分线,交BC于点D;(要求:不写作法,保留作图痕迹)
(2)求S△ADC: S△ADB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足,下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=EF=EC;④AE=EC,其中正确的是________(填序号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com