
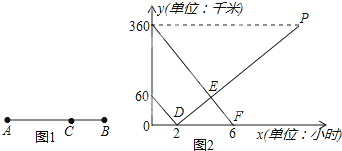
分析 (1)根据函数图象可以得到A,B两地的距离;
(2)根据图象中的数据可以求得两小时后,货车离C站的路程y2与行驶时间x之间的函数关系式;
(3)根据函数图象可以求得客车离C站的路程y1与行驶时间x之间的函数关系式,然后与(2)中的函数解析式联立方程组即可解答本题.
解答 解:(1)由题意和图象可得,
A,B两地相距:360+60=420千米,
故答案为:420;
(2)设两小时后,货车离C站的路程y2与行驶时间x之间的函数关系式为y2=kx+b,
由图象可得,货车的速度为:60÷2=30千米/时,
则点P的横坐标为:2+360÷30=14,
∴点P的坐标为(14,360),
$\left\{\begin{array}{l}{2k+b=0}\\{14k+b=360}\end{array}\right.$,得$\left\{\begin{array}{l}{k=30}\\{b=-60}\end{array}\right.$,
即两小时后,货车离C站的路程y2与行驶时间x之间的函数关系式为y2=30x-60;
(3)设客车离C站的路程y1与行驶时间x之间的函数关系式为:y1=mx+n,
$\left\{\begin{array}{l}{n=360}\\{6m+n=0}\end{array}\right.$,得$\left\{\begin{array}{l}{m=-60}\\{n=360}\end{array}\right.$,
即客车离C站的路程y1与行驶时间x之间的函数关系式为:y1=-60x+360,
∴$\left\{\begin{array}{l}{-60x+360=y}\\{30x-60=y}\end{array}\right.$,得$\left\{\begin{array}{l}{x=\frac{14}{3}}\\{y=80}\end{array}\right.$,
即客、货两车在$\frac{14}{3}$时相遇,此时相遇处离C站的路程是80千米.
点评 本题考查一次函数的应用,解答此类问题的关键是明确题意,求出相应的函数解析式,利用数形结合的思想解答问题.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{a+b}{2}$元 | B. | (am+bn)%元 | C. | $\frac{am+bn}{a+b}$元 | D. | $\frac{am+bn}{m+n}$元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某中学教学楼的后面靠近一座山坡,坡面下是一块草地,如图所示,BC∥AD,斜坡AB=160米,坡度i=$\sqrt{3}$:1,为防止山体滑坡,保障学生安全,学校决定不仅加固教学楼,还对山坡进行改造,当坡角不超过45°时可保证山体不滑坡,改造时保持坡脚A不动,从坡顶B沿BC进到E处,问BE至少是多少米?(结果保留根号)
某中学教学楼的后面靠近一座山坡,坡面下是一块草地,如图所示,BC∥AD,斜坡AB=160米,坡度i=$\sqrt{3}$:1,为防止山体滑坡,保障学生安全,学校决定不仅加固教学楼,还对山坡进行改造,当坡角不超过45°时可保证山体不滑坡,改造时保持坡脚A不动,从坡顶B沿BC进到E处,问BE至少是多少米?(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
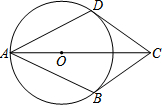 如图,已知在四边形ABCD中,AB=AD,BC=CD,点O在对角线AC上,以O为圆心OA为半径的⊙O与CD相切于点D.
如图,已知在四边形ABCD中,AB=AD,BC=CD,点O在对角线AC上,以O为圆心OA为半径的⊙O与CD相切于点D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com