
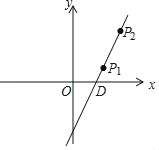
【题目】如图,直线l上有一点P1(2,1),将点P1先向右平移1个单位,再向上平移2个单位得到像点P2,点P2恰好在直线l上.
(1)点P2的坐标为 ;
(2)求直线l的解析表达式;
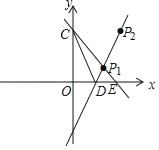
(3)求直线y=﹣x+b经过点P1,交x轴于点C,则b的值是多少?已知直线l与x轴交于点D,求△P1CD的面积是多少?
【答案】(1)(3,3).(2)y=2x﹣3.(3)![]() .
.
【解析】分析:(1)根据“右加左减、上加下减”的规律来求点P2的坐标;
(2)设直线l所表示的一次函数的表达式为y=kx+b(k≠0),把点P1(2,1),P2(3,3)代入直线方程,利用方程组来求系数的值;
(3)根据点P1的坐标可求出b值,进而得出C、E的坐标,利用一次函数图象上点的坐标特征可求出点D的坐标,再根据三角形的面积公式结合![]() =S△COE﹣S△COD﹣
=S△COE﹣S△COD﹣![]() 即可求出△P1CD的面积.
即可求出△P1CD的面积.
详解:(1)∵将点P1先向右平移1个单位,再向上平移2个单位得到像点P2,点P1的坐标为(2,1),
∴点P2的坐标为(3,3).
故答案为:(3,3).
(2)设直线l的解析表达式为y=mx+n(m≠0),
将P1(2,1)、P2(3,3)代入y=mx+n,
得![]() ,解得:
,解得:![]() ,
,
∴直线l的解析表达式为y=2x﹣3.
(3)∵求直线y=﹣x+b经过点P1(2,1),
∴1=﹣2+b,
∴b=3,
∴直线CP1的解析表达式为y=﹣x+3,
∴点C的坐标为(0,3).
设直线CP1的x轴的交点为E,则点E(3,0).
当y=0时,有2x﹣3=0,
解得:x=![]() ,
,
∴点D的坐标为(![]() ,0),
,0),
∴![]() =S△COE﹣S△COD﹣
=S△COE﹣S△COD﹣![]() =
=![]() ×3×3﹣
×3×3﹣![]() ×3×
×3×![]() ﹣
﹣![]() ×
×![]() ×1=
×1=![]() .
.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:
【题目】怡然美食店的A、B两种菜品,每份成本均为14元,售价分别为20元、18元,这两种菜品每天的营业额共为1120元,总利润为280元.
(1)该店每天卖出这两种菜品共多少份?
(2)该店为了增加利润,准备降低A种菜品的售价,同时提高B种菜品的售价,售卖时发现,A种菜品售价每降0.5元可多卖1份;B种菜品售价每提高0.5元就少卖1份,如果这两种菜品每天销售总份数不变,那么这两种菜品一天的总利润最多是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y=![]() .
.
(1)若该反比例函数的图象与直线y=kx+4(k≠0)只有一个公共点,求k的值;
(2)如图,反比例函数y=![]() (1≤x≤4)的图象记为曲线C1,将C1向左平移2个单位长度,得曲线C2,请在图中画出C2,并直接写出C1平移到C2处所扫过的面积.
(1≤x≤4)的图象记为曲线C1,将C1向左平移2个单位长度,得曲线C2,请在图中画出C2,并直接写出C1平移到C2处所扫过的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△AOB中,AB⊥OB,且AB=OB=3,设直线![]() 截此三角形所得阴影部分的面积为S,则S与t之间的函数关系的图象为下列选项中的( )
截此三角形所得阴影部分的面积为S,则S与t之间的函数关系的图象为下列选项中的( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线y=x2+bx+c过A,B,C三点,点A的坐标是(3,0),点C的坐标是(0,-3),动点P在抛物线上.
(1)b =_________,c =_________,点B的坐标为_____________;(直接填写结果)
(2)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(3)过动点P作PE垂直y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从A,B,C三个厂家生产的同一种产品中各抽出8件产品,对其使用寿命进行跟踪调查,结果(单位:年)如下:
A.3,4,5,6,8,8,8,10;
B.5,6,6,6,8,8,12,13;
C.3,3,4,7,9,10,11,12.
三个厂家在广告中都称该种产品的使用寿命为8年,请根据调查结果判断厂家在广告中分别运用了平均数、中位数、众数中的哪一个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,![]() 、
、![]() 在数轴上对应的数分别用
在数轴上对应的数分别用![]() 、
、![]() 表示,且
表示,且![]() .
.
![]()
(1)数轴上点![]() 表示的数是________,点
表示的数是________,点![]() 表示的数是___________;
表示的数是___________;
(2)若一动点![]() 从点
从点![]() 出发,以
出发,以![]() 个单位长度秒速度由
个单位长度秒速度由![]() 向
向![]() 运动;动点
运动;动点![]() 从原点
从原点![]() 出发,以
出发,以![]() 个单位长度
个单位长度![]() 秒速度向
秒速度向![]() 运动,点
运动,点![]() 、
、![]() 同时出发,点
同时出发,点![]() 运动到
运动到![]() 点时两点同时停止.设点
点时两点同时停止.设点![]() 运动时间为
运动时间为![]() 秒.
秒.
①若![]() 从
从![]() 到
到![]() 运动,则
运动,则![]() 点表示的数为_______,
点表示的数为_______,![]() 点表示的数为___________(用含
点表示的数为___________(用含![]() 的式子表示)
的式子表示)
②当![]() 为何值时,点
为何值时,点![]() 与点
与点![]() 之间的距离为
之间的距离为![]() 个单位长度.
个单位长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
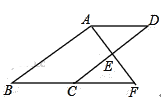
【题目】如图,E是ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:△ADE≌△FCE;
(2)若AB⊥AF,BC=12,EF=6,求CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com