
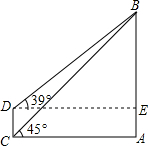
 目前世界上最高的电视塔是广州新电视塔.如图所示,新电视塔高AB为610米,远处有一栋大楼,某人在楼底C处测得塔顶B的仰角为45°,在楼顶D处测得塔顶B的仰角为39°,(sin39°≈0.63,cos39°≈0.78,tan39°≈0.81)
目前世界上最高的电视塔是广州新电视塔.如图所示,新电视塔高AB为610米,远处有一栋大楼,某人在楼底C处测得塔顶B的仰角为45°,在楼顶D处测得塔顶B的仰角为39°,(sin39°≈0.63,cos39°≈0.78,tan39°≈0.81)分析 (1)判断出△BAC为等腰直角三角形,即可求出AC的长;
(2)在Rt△DEB中,根据$\frac{BE}{DE}$=tan39°即可求出CD的长.
解答 解:(1)∵塔顶B的仰角为45°,
∴∠ABC=∠ACB=45°,
∴AC=AB=610米;
(2)根据题意可知四边形ACDE为矩形,
则AC=DE,设AE=DC=x米,
则BE=(610-x)米,
在Rt△DEB中,$\frac{BE}{DE}$=tan39°,
∴$\frac{610-x}{610}$≈0.81,
解得x≈116.
答:大楼与电视塔之间的距离AC为610米,大楼的高CD为116米.
点评 本题考查了解直角三角形的应用---仰角俯角问题,熟悉等腰三角形的性质和三角函数的定义是解题的关键.


 能力评价系列答案
能力评价系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
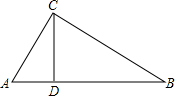 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若BC=$\sqrt{5}$,AC=2,则sin∠ACD的值为( )
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若BC=$\sqrt{5}$,AC=2,则sin∠ACD的值为( )| A. | $\frac{\sqrt{5}}{3}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
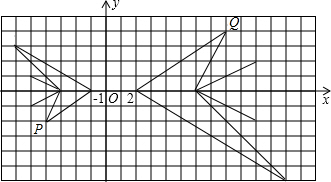 某学习小组在讨论“变化的鱼”,已知如图中的大鱼与小鱼是以原点O为位似中心的位似图形,且大鱼与小鱼的位似比是2:1,若小鱼上的点P(a,b),对应大鱼上的点Q,则点Q的坐标为( )
某学习小组在讨论“变化的鱼”,已知如图中的大鱼与小鱼是以原点O为位似中心的位似图形,且大鱼与小鱼的位似比是2:1,若小鱼上的点P(a,b),对应大鱼上的点Q,则点Q的坐标为( )| A. | (-2a,-2b) | B. | (-a,-2b) | C. | (-2b,-2a) | D. | (-2a,-b) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
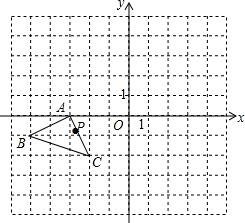 如图,在平面直角坐标系中,P(a,b)是△ABC的边AC上一点,△ABC经平移得到△A1B1C1,且点P的对应点为P1(a+5,b+4).
如图,在平面直角坐标系中,P(a,b)是△ABC的边AC上一点,△ABC经平移得到△A1B1C1,且点P的对应点为P1(a+5,b+4).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com