练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】请将下列证明过程补充完整：

    已知：如图，点P在CD上，已知∠BAP+∠APD=180°，∠1=∠2

    求证：∠E=∠F

    证明：∵∠BAP+∠APD=180°（已知）

    ∴ ∥ （ ）

    ∴∠BAP= （ ）

    又∵∠1=∠2（已知）

    ∴∠BAP﹣ = ﹣∠2

    即∠3= （等式的性质）

    ∴AE∥PF（ ）

    ∴∠E=∠F（ ）

    【答案】答案见解析

    【解析】分析：根据平行线的性质以及判定定理进行填空即可得出答案．

    详解：∵∠BAP+∠APD=180°（已知）

    ∴ AB∥ CD（同旁内角互补，两直线平行 ）

    ∴∠BAP= ∠APC （两直线平行，内错角相等 ）

    又∵∠1=∠2（已知）

    ∴∠BAP﹣ ∠1 = ∠APC ﹣∠2

    即∠3= ∠4 （等式的性质）

    ∴AE∥PF（内错角相等，两直线平行 ）

    ∴∠E=∠F（两直线平行，内错角相等 ）

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

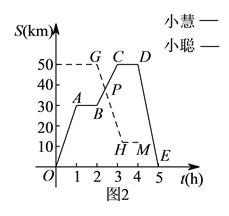
    【题目】小聪和小慧在某风景区（如图）沿景区公路游览，约好在宾馆见面．上午，小慧乘坐车速为的电动汽车从宾馆出发，先后在两个景点游玩分钟和分钟后回到宾馆．小聪骑自行车从飞瀑出发，车速为，他先后在两个景点游玩了分钟和分钟后回到宾馆．图中的图象分别表示小慧和小聪离宾馆的路程与时间的函数关系（不全）．试结合图中信息回答：

    （）小慧游览的景点是__________，点的坐标为__________．

    （）当小聪和小慧相遇时，叫他们距离宾馆多少千米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，∠EAC＝90°，∠1＋∠2＝90°，∠1＝∠3，∠2＝∠4.

    (1)如图①，求证：DE∥BC；

    (2)若将图①改变为图②，其他条件不变，(1)中的结论是否仍成立？请说明理由．

    如图，∠EAC＝90°，∠1＋∠2＝90°，∠1＝∠3，∠2＝∠4.

    (1)如图①，求证：DE∥BC；

    (2)若将图①改变为图②，其他条件不变，(1)中的结论是否仍成立？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在ABCD中，BD是对角线，AE⊥BD于点E，CF⊥BD于点F，试判断四边形AECF是不是平行四边形，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】二次函数 的图像如图所示，点A0位于坐标原点，点A1 ， A2 ， A3 ， …，A2008在y轴的正半轴上，点B1 ， B2 ， B3 ， …，B2008在二次函数 位于第一象限的图像上，若△A0B1A1 ， △A1B2A2 ， △A2B3A3 ， …，△A2007B2008A2008都为等边三角形，则△A2007B2008A2008的边长=

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读理解题：

    定义：如果一个数的平方等于-1，记为，这个数叫做虚数单位。那么和我们所学的实数对应起来就叫做复数，表示为（， 为实数），叫这个复数的实部， 叫做这个复数的虚部，它的加，减，乘法运算与整式的加，减，乘法运算类似。

    例如计算：

    （1）填空： =_________， =____________；

    （2）计算： ；

    （3）计算：

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】请把下面证明过程补充完整：

    已知：如图，∠ADC=∠ABC，BE、DF分别平分∠ABC、∠ADC，且∠1=∠2．

    求证：∠A=∠C．

    证明：∵BE、DF分别平分∠ABC、∠ADC(已知)，

    ∴∠1=∠ABC，∠3=∠ADC(角平分线定义)．

    ∵∠ABC=∠ADC(已知)，

    ∴∠1=∠3(等量代换)，

    ∵∠1=∠2(已知)，

    ∴∠2=∠3(等量代换)．

    ∴_____∥_____ (___ __)．

    ∴∠A+∠_____=180°，∠C+∠_____=180°(___ __)．

    ∴∠A=∠C(___ __)．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】问题情境：如图1，AB∥CD，∠PAB=130°，∠PCD=120°．求∠APC度数．

    小明的解题思路是：如图2，过P作PE∥AB，通过平行线性质，可得∠APC=50°+60°=110°．

    问题迁移：

    （1）如图3，AD∥BC，点P在射线OM上运动，当点P在A、B两点之间运动时，∠ADP=∠α，∠BCP=∠β．试判断∠CPD、∠α、∠β之间有何数量关系？请说明理由；

    （2）在（1）的条件下，如果点P在A、B两点外侧运动时（点P与点A、B、O三点不重合），请你直接写出∠CPD、∠α、∠β间的数量关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我们在计算(2+1)(22+1)(24+1)(28+1)(216+1)时，发现直接运算很麻烦，如果在算式前乘以(2-1)，即1，原算式的值不变，而且还使整个算式是能用乘法公式计算.

    即：原式=(2-1) (2+1)(22+1)(24+1)(28+1)(216+1)=232-1.

    请用上述方法算出(5+1) (52+1)(54+1)(58+1)(516+1) (532+1)的值为_________.

    查看答案和解析>>

    同步练习册答案