
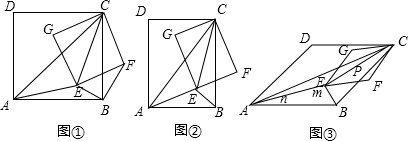
分析 (1)(i)首先根据四边形ABCD和EFCG均为正方形,可得$\frac{AC}{BC}=\frac{CE}{CF}=\sqrt{2}$,∠ACE=∠BCF;然后根据相似三角形判定的方法,推得△CAE∽△CBF即可.
(ii)首先根据△CAE∽△CBF,判断出∠CAE=∠CBF,再根据∠CAE+∠CBE=90°,判断出∠EBF=90°;然后在Rt△BEF中,根据勾股定理,求出EF的长度,再根据CE、EF的关系,求出CE的长是多少即可.
(2)首先根据相似三角形判定的方法,判断出△ACE∽△BCF,即可判断出$\frac{AE}{BF}=\frac{AC}{BC}=\sqrt{{k}^{2}+1}$,据此求出BF的长度是多少;然后判断出∠EBF=90°,在Rt△BEF中,根据勾股定理,求出EF的值是多少,进而求出k的值是多少即可.
(3)首先根据∠DAB=45°,可得∠ABC=180°-45°=135°,在△ABC中,根据勾股定理可求得AB2、BC2,AC2之间的关系,EF2、FC2,EC2之间的关系;然后根据相似三角形判定的方法,判断出△ACE∽△BCF,即可用n表示出BF的值;最后判断出EBF=90°,在Rt△BEF中,根据勾股定理,判断出m,n,p三者之间满足的等量关系即可.
解答 (1)(i)证明:∵四边形ABCD和EFCG均为正方形,
∴$\frac{AC}{BC}=\frac{CE}{CF}=\sqrt{2}$,
∴∠ACB=∠ECF=45°,
∴∠ACE=∠BCF,
在△CAE和△CBF中,
$\left\{\begin{array}{l}{\frac{AC}{BC}=\frac{CE}{CF}=\sqrt{2}}\\{∠ACE=∠BCF}\end{array}\right.$,
∴△CAE∽△CBF.
(ii)解:∵△CAE∽△CBF,
∴∠CAE=∠CBF,$\frac{AE}{BF}=\frac{AC}{BC}$,
又∵∠CAE+∠CBE=90°,
∴∠CBF+∠CBE=90°,
∴∠EBF=90°,
又∵$\frac{AE}{BF}=\frac{AC}{BC}=\sqrt{2}$,AE=2
∴$\frac{2}{BF}=\sqrt{2}$,
∴$BF=\sqrt{2}$,
∴EF2=BE2+BF2=${1}^{2}{+(\sqrt{2})}^{2}$=3,
∴EF=$\sqrt{3}$,
∵CE2=2EF2=6,
∴CE=$\sqrt{6}$.
(2)如图②,连接BF,
∵$\frac{AB}{BC}$=$\frac{EF}{FC}$=k,
∴BC=a,AB=ka,FC=b,EF=kb,
∴AC=$\sqrt{{AB}^{2}{+BC}^{2}}=\sqrt{{{k}^{2}a}^{2}{+a}^{2}}=a\sqrt{{k}^{2}+1}$,
CE=$\sqrt{{EF}^{2}{+FC}^{2}}$=$\sqrt{{{k}^{2}b}^{2}{+b}^{2}}=b\sqrt{{k}^{2}+1}$,
∴$\frac{AC}{BC}=\frac{EC}{FC}=\sqrt{{k}^{2}+1}$,∠ACE=∠BCF,
在△ACE和△BCF中,
$\left\{\begin{array}{l}{\frac{AC}{BC}=\frac{EC}{FC}=\sqrt{{k}^{2}+1}}\\{∠ACE=∠BCF}\end{array}\right.$,
∴△ACE∽△BCF,
∴$\frac{AE}{BF}=\frac{AC}{BC}=\sqrt{{k}^{2}+1}$,∠CAE=∠CBF,
又∵AE=2,
∴$\frac{2}{BF}=\sqrt{{k}^{2}+1}$,
∴BF=$\frac{2}{\sqrt{{k}^{2}+1}}$,
∵∠CAE=∠CBF,∠CAE+∠CBE=90°,
∴∠CBE+∠CBF=90°,
∴∠EBF=90°,
∴EF2=BE2+BF2=1$+\frac{4}{{k}^{2}+1}$,
∵$\frac{EC}{FC}=\sqrt{{k}^{2}+1}$,
∴$\frac{CE}{EF}$=$\frac{\sqrt{{k}^{2}+1}}{k}$,CE=3,
∴EF=$\frac{3k}{\sqrt{{k}^{2}+1}}$,
∴1$+\frac{4}{{k}^{2}+1}{=(\frac{3k}{\sqrt{{k}^{2}+1}})}^{2}=\frac{{9k}^{2}}{{k}^{2}+1}$,
∴${k}^{2}=\frac{5}{8}$,
解得k=±$\frac{\sqrt{10}}{4}$,
∵$\frac{AB}{BC}$=$\frac{EF}{FC}$=k>0,
∴k=$\frac{\sqrt{10}}{4}$.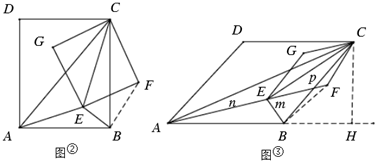
(3)连接BF,同理可得∠EBF=90°,过C点作CH⊥AB延长线于H,
∵四边形ABCD为菱形,
∴AB=BC,设AB=BC=x,
∵∠CBH=∠DAB=45°,∴BH=CH=$\frac{\sqrt{2}}{2}$x,
∴AC2=AH2+CH2=(x+$\frac{\sqrt{2}}{2}$x)2+($\frac{\sqrt{2}}{2}$x)2,=(2+$\sqrt{2}$)x2,
∴AB2:BC2:AC2=1:1:(2+$\sqrt{2}$),
同理可得EF2:FC2:EC2=1:1:(2+$\sqrt{2}$),
∴EF2=$\frac{E{C}^{2}}{2+\sqrt{2}}$=$\frac{{p}^{2}}{2+\sqrt{2}}$,
在△ACE和△BCF中,
$\left\{\begin{array}{l}{\frac{AC}{BC}=\frac{EC}{FC}=\sqrt{2+\sqrt{2}}}\\{∠ACE=∠BCF}\end{array}\right.$,
∴△ACE∽△BCF,
∴$\frac{A{E}^{2}}{B{F}^{2}}$=$\frac{A{C}^{2}}{B{C}^{2}}$=2+$\sqrt{2}$,∠CAE=∠CBF,
又∵AE=n,
∴${BF}^{2}=\frac{{AE}^{2}}{2+\sqrt{2}}=\frac{{n}^{2}}{2+\sqrt{2}}$,
∵∠CAE=∠CBF,∠CAE+∠CBE=90°,
∴∠CBE+∠CBF=90°,
∴∠EBF=90°,
∴EF2=BE2+BF2,
∴$\frac{{p}^{2}}{2+\sqrt{2}}{=m}^{2}+\frac{{n}^{2}}{2+\sqrt{2}}$,
∴(2$+\sqrt{2}$)m2+n2=p2,
即m,n,p三者之间满足的等量关系是:(2$+\sqrt{2}$)m2+n2=p2.
点评 (1)此题主要考查了四边形综合题,考查了分析推理能力,考查了空间想象能力,考查了数形结合方法的应用,要熟练掌握.
(2)此题还考查了相似三角形的判定和性质的应用,要熟练掌握.
(3)此题还考查了直角三角形的性质和应用,以及勾股定理的应用,要熟练掌握.


科目:初中数学 来源: 题型:解答题
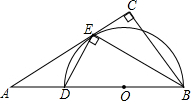 如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,点D在AB边上且DE⊥BE.
如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,点D在AB边上且DE⊥BE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
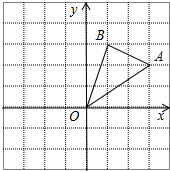 如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).△AOB绕点O逆时针旋转90°后得到△A1OB1.
如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).△AOB绕点O逆时针旋转90°后得到△A1OB1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
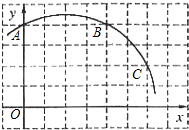 如图,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C.
如图,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
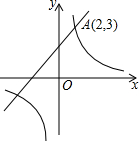 如图,一次函数y1=k1x+b(k1、b为常数,且k1≠0)的图象与反比例函数y2=$\frac{{k}_{2}}{x}$(k2为常数,且k2≠0)的图象都经过点A(2,3).则当x>2时,y1与y2的大小关系为y1>y2.
如图,一次函数y1=k1x+b(k1、b为常数,且k1≠0)的图象与反比例函数y2=$\frac{{k}_{2}}{x}$(k2为常数,且k2≠0)的图象都经过点A(2,3).则当x>2时,y1与y2的大小关系为y1>y2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
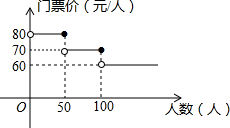 我市某风景区门票价格如图所示,黄冈赤壁旅游公司有甲、乙两个旅游团队,计划在“五一”小黄金周期间到该景点游玩.两团队游客人数之和为120人,乙团队人数不超过50人,设甲团队人数为x人.如果甲、乙两团队分别购买门票,两团队门票款之和为W元.
我市某风景区门票价格如图所示,黄冈赤壁旅游公司有甲、乙两个旅游团队,计划在“五一”小黄金周期间到该景点游玩.两团队游客人数之和为120人,乙团队人数不超过50人,设甲团队人数为x人.如果甲、乙两团队分别购买门票,两团队门票款之和为W元.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
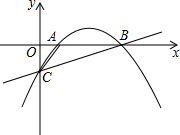 如图,抛物线y=ax2+bx-$\frac{5}{3}$经过点A(1,0)和点B(5,0),与y轴交于点C.
如图,抛物线y=ax2+bx-$\frac{5}{3}$经过点A(1,0)和点B(5,0),与y轴交于点C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com