
分析 利用内角和的公式,挖掘此题隐含着边数为正整数这个条件,用不等式确定范围后求解.
解答 解:设∠A,∠B,∠C均为钝角,
则90°<A<180°,90°<B<180°,90°<C<180°.
270°<A+B+C<540°.
n边形中其余n-3个角均小于等于90°.
∵∠A+∠B+∠C+∠D+…+∠N<540°+(n-3)×90°,
n边形的n个角和为(n-2)×180°,
∴(n-2)180°<540°+(n-3)×90°,
推出:n<7,
∴n的最大值为6.
内角只有3个钝角,对应的外角为锐角;其他的内角则为直角或锐角,对应的外角则为直角或钝角
由外角定理:3锐角+n(直角或钝角)=360°
要使n尽可能小,那么3个锐角尽量大(如89°),那么只要一个钝角就行了,n=1,多边形边数为4
综上,多边形边数最小值为4,最大值为6.
点评 本题主要考查了多边形的外角和定理以及不等式的应用,得出(n-2)×180°<540°+(n-3)×90°是解题关键.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:选择题
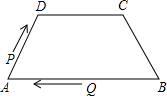 如图,在四边形ABCD中,AB∥DC,AD=BC=5,DC=7,AB=13,点P从点A出发以3个单位/s的速度沿AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA向终点A运动.当四边形PQBC为平行四边形时,运动时间为( )
如图,在四边形ABCD中,AB∥DC,AD=BC=5,DC=7,AB=13,点P从点A出发以3个单位/s的速度沿AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA向终点A运动.当四边形PQBC为平行四边形时,运动时间为( )| A. | 4s | B. | 3s | C. | 2s | D. | 1s |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com