
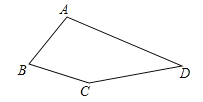
【题目】如图,在四边形ABCD中,∠B=60°,∠D=30°,AB=BC.
(1)求∠A+∠C的度数;
(2)连接BD,探究AD,BD,CD三者之间的数量关系,并说明理由;
(3)若AB=1,点E在四边形ABCD内部运动,且满足AE2=BE2+CE2,求点E运动路径的长度.
【答案】(1)270°;(2)DB2=DA2+DC2;(3)![]() .
.
【解析】
(1)利用四边形内角和定理计算即可;
(2)连接BD.以BD为边向下作等边三角形△BDQ.想办法证明△DCQ是直角三角形即可解决问题;
(3)如图3中,连接AC,将△ACE绕点A顺时针旋转60°得到△ABR,连接RE.想办法证明∠BEC=150°即可解决问题.
(1)如图1中,
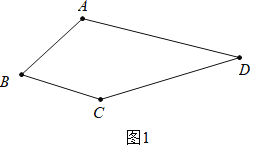
在四边形ABCD中,
∵∠A+∠B+∠C+∠D=360°,∠B=60°,∠C=30°,
∴∠A+∠C=360°﹣60°﹣30°=270°;
(2)如图2中,结论:DB2=DA2+DC2,
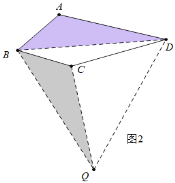
理由:连接BD,以BD为边向下作等边三角形△BDQ,
∵∠ABC=∠DBQ=60°,
∴∠ABD=∠CBQ,
∵AB=BC,DB=BQ,
∴△ABD≌△CBQ,
∴AD=CQ,∠A=∠BCQ,
∵∠A+∠BCD=∠BCQ+∠BCD=270°,
∴∠DCQ=90°,
∴DQ2=DC2+CQ2,
∵CQ=DA,DQ=DB,
∴DB2=DA2+DC2;
(3)如图3中,
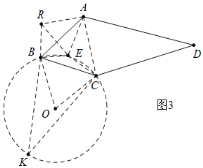
连接AC,将△ACE绕点A顺时针旋转60°得到△ABR,连接RE,则△AER是等边三角形,
∵EA2=EB2+EC2,EA=RE,EC=RB,
∴RE2=RB2+EB2,
∴∠EBR=90°,
∴∠RAE+∠RBE=150°,
∴∠ARB+∠AEB=∠AEC+∠AEB=210°,
∴∠BEC=150°,
∴点E的运动轨迹在O为圆心的圆上,在⊙O上取一点K,连接KB,KC,OB,OC,
∵∠K+∠BEC=180°,
∴∠K=30°,∠BOC=60°,
∵OB=OC,
∴△OBC是等边三角形,
∴点E的运动路径![]() .
.


科目:初中数学 来源: 题型:
【题目】已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.
(1)求证:AB=AC;
(2)若AB=4,BC=![]() ,求CD的长.
,求CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,海中有一小岛P,在距小岛P的![]() 海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?
海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着移动互联网的快速发展,基于互联网的共享单车应运而生.为了解某小区居民使用共享单车的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数分别为:17,12,15,20,17,0,7,26,17,9.
(1)这组数据的中位数是 ,众数是 ;
(2)计算这10位居民一周内使用共享单车的平均次数;
(3)若该小区有200名居民,试估计该小区居民一周内使用共享单车的总次数.
查看答案和解析>>
科目:初中数学 来源: 题型:
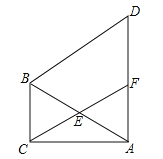
【题目】如图,在△ABC中,∠ACB=90°,∠CAB=30°,以线段AB为边向外作等边△ABD,点E是线段AB的中点,连接CE并延长交线段AD于点F.
(1)求证:四边形BCFD为平行四边形;
(2)若AB=6,求平行四边形BCFD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名在校大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于16元/件,市场调查发现,该产品每天的销售量![]() (件
(件![]() 与销售价
与销售价![]() (元/件)之间的函数关系如图所示.
(元/件)之间的函数关系如图所示.
(1)求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)求每天的销售利润W(元![]() 与销售价
与销售价![]() (元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?
(元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象对称轴为x=![]() ,图象交x轴于A,B,交y轴于C(0,-3),且AB=5,直线y=kx+b(k>0)与二次函数图象交于M,N(M在N的右边),交y轴于P.
,图象交x轴于A,B,交y轴于C(0,-3),且AB=5,直线y=kx+b(k>0)与二次函数图象交于M,N(M在N的右边),交y轴于P.
(1)求二次函数图象的解析式;
(2)若b=-5,且△CMN的面积为3,求k的值;
(3)若b=-3k,直线AN交y轴于Q,求![]() 的值或取值范围.
的值或取值范围.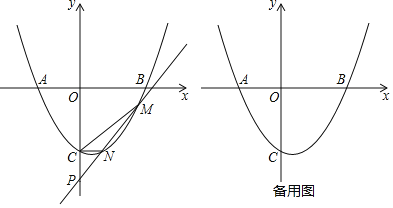
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com