
【题目】已知二次函数y=ax2+bx+c的图象对称轴为x=![]() ,图象交x轴于A,B,交y轴于C(0,-3),且AB=5,直线y=kx+b(k>0)与二次函数图象交于M,N(M在N的右边),交y轴于P.
,图象交x轴于A,B,交y轴于C(0,-3),且AB=5,直线y=kx+b(k>0)与二次函数图象交于M,N(M在N的右边),交y轴于P.
(1)求二次函数图象的解析式;
(2)若b=-5,且△CMN的面积为3,求k的值;
(3)若b=-3k,直线AN交y轴于Q,求![]() 的值或取值范围.
的值或取值范围.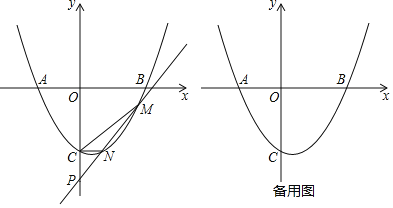
【答案】(1)![]() ;(2)k=2;(3)
;(2)k=2;(3)![]() ≥
≥![]() .
.
【解析】
(1)由图象对称轴为x=![]() ,AB=5,知:A(-2,0)、B(0,-3),把A、B、C点坐标代入二次函数即可求解;
,AB=5,知:A(-2,0)、B(0,-3),把A、B、C点坐标代入二次函数即可求解;
(2)S△CMN=![]() HNxM=6,用根与系数的关系求解即可;
HNxM=6,用根与系数的关系求解即可;
(3)求出xN=![]() ,分2k-5>0时和2k-5<0两种情况,求出点Q坐标即可求解.
,分2k-5>0时和2k-5<0两种情况,求出点Q坐标即可求解.
(1)由图象对称轴为x=![]() ,AB=5,知:A(-2,0)、B(0,-3),
,AB=5,知:A(-2,0)、B(0,-3),
把A、B、C点坐标代入二次函数表达式得:a=![]() ,b=-
,b=-![]() ,c=-3;
,c=-3;
故函数表达式为:y=![]() x2-
x2-![]() x-3…①;
x-3…①;
(2)b=-5,直线MN表达式为:y=kx-5…②,
设:M(x1,y1),N(x2,y2),
将①、②联立并整理得:x2-(2k+1)x+4=0,
则:x1+x2=2k+1,x1x2=4,
直线C(0,-3)、M(x1,y1)所在的直线方程为:
y=![]() ,
,
过N点做直线HM∥y轴,交MC于H,则H(x1,![]() x13),
x13),
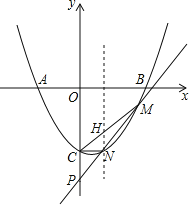
S△CMN=![]() HNxM=6,
HNxM=6,
整理得:x1y2-x2y1+3x1-3x2=6,
把y1=3x1-5,y2=3x2-5,代入上式整理得:
x2-x1=3,
即:(x1+x2)2-4x1x2=9,
k=2;
(3)b=-3k,直线y=kx+b=kx-3k…③,
将①、③方程联立并整理得:
x2-(2k+1)x+(6k-6)=0,
△=4k2-20k+25=(2k-5)2>0,
xN=![]() ,
,
当2k-5>0时,
xN=3,则N(3,0),
而Q(0,0),P(0,-3k),C(0,-3)
则:CP=3k-3,CQ=3,
∴![]() =k-1,即:
=k-1,即:![]() >
>![]() ;
;
当2k-5<0时,
xN=2k-2,则N(2k-2,2k2-5k),
则AN所在的直线方程为:y=![]() x+(2k5),
x+(2k5),
则:Q(0,2k-5),
而C(0,-3)P(0,-3k),
则:CP=3k-3,CQ=2k-2,
∴![]() =
=![]() ,
,
故:![]() ≥
≥![]() .
.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:初中数学 来源: 题型:
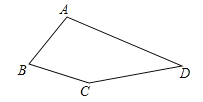
【题目】如图,在四边形ABCD中,∠B=60°,∠D=30°,AB=BC.
(1)求∠A+∠C的度数;
(2)连接BD,探究AD,BD,CD三者之间的数量关系,并说明理由;
(3)若AB=1,点E在四边形ABCD内部运动,且满足AE2=BE2+CE2,求点E运动路径的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解一路段车辆行驶速度的情况,交警统计了该路段上午7::0至9:00来往车辆的车速(单位:千米/时),并绘制成如图所示的条形统计图.这些车速的众数、中位数分别是( )
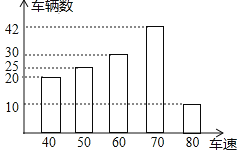
A. 众数是80千米![]() 时,中位数是60千米
时,中位数是60千米![]() 时
时
B. 众数是70千米![]() 时,中位数是70千米
时,中位数是70千米![]() 时
时
C. 众数是60千米![]() 时,中位数是60千米
时,中位数是60千米![]() 时
时
D. 众数是70千米![]() 时,中位数是60千米
时,中位数是60千米![]() 时
时
查看答案和解析>>
科目:初中数学 来源: 题型:
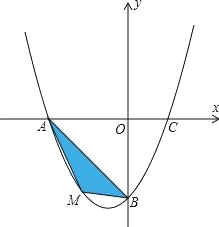
【题目】在平面直角坐标系中,已知抛物线y=![]() +bx﹣4经过A(﹣4,0),C(2,0)两点.
+bx﹣4经过A(﹣4,0),C(2,0)两点.
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值;
(3)若点P是抛物线上的动点,点Q是直线y=﹣x上的动点,点B是抛物线与y轴交点.判断有几个位置能够使以点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
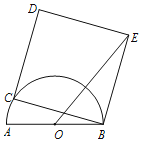
【题目】如图,点C是半圆![]() 上一动点,以BC为边作正方形BCDE,使
上一动点,以BC为边作正方形BCDE,使![]() 在正方形内,连OE,若AB=4cm,则OD的最大值为_____________cm.
在正方形内,连OE,若AB=4cm,则OD的最大值为_____________cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年5月31日是世界卫生组织发起的第31个“世界无烟日”.重庆育才中学学生处鼓励学生积极宣传,并设计调查问卷,以更好地宣传吸烟的危害,七年级58班数学兴趣小组第一组的5名同学设计了如下调查问卷,随机调查了部分吸烟人,并将调查结果绘制成统计图.
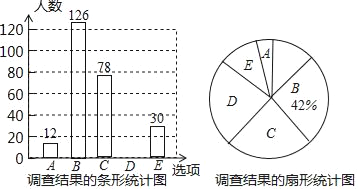
根据以上信息,解答下列问题:
(1)E选项所在扇形的圆心角的度数是 ,并把条形统计图补充完整.
(2)重庆育才中学七年级58班数学兴趣小组第一组的5名同学中有两名男同学们,学校学生处准备从七年级58班数学兴趣小组第一组的5名同学中选取两名同学参加“世界无烟日”活动的总结会,请你用列表法或画树状图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
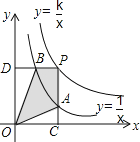
【题目】反比例函数y=![]() 和y=
和y=![]() 在第一象限内的图象如图所示,点P在y=
在第一象限内的图象如图所示,点P在y=![]() 的图象上,PC⊥x轴,交y=
的图象上,PC⊥x轴,交y=![]() 的图象于点A,PD⊥y轴,交y=
的图象于点A,PD⊥y轴,交y=![]() 的图象于点B.当点P在y=
的图象于点B.当点P在y=![]() 的图象上运动时,以下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积不会发生变化;④当点A是PC的中点时,点B一定是PD的中点.其中一定正确的是( )
的图象上运动时,以下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积不会发生变化;④当点A是PC的中点时,点B一定是PD的中点.其中一定正确的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工艺品厂生产一种汽车装饰品,每件生产成本为20元,销售价格在30元至80元之间(含30元和80元),销售过程中的管理、仓储、运输等各种费用(不含生产成本)总计50万元,其销售量y(万个)与销售价格(元/个)的函数关系如图所示.
(1)当30≤x≤60时,求y与x的函数关系式;
(2)求出该厂生产销售这种产品的纯利润w(万元)与销售价格x(元/个)的函数关系式;
(3)销售价格应定为多少元时,获得利润最大,最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
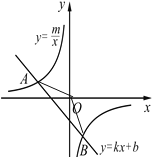
【题目】如图,已知A(-4,2)、B(n,-4)是一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象的两个交点.
的图象的两个交点.
(1)求此反比例函数和一次函数的解析式;
(2)求△AOB的面积;
(3)根据图象写出使一次函数的值小于反比例函数的值的x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com