
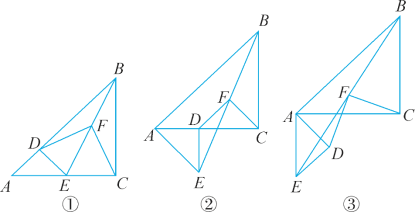
【题目】已知△ABC和△ADE是等腰直角三角形,∠ACB=∠ADE=90°,F为BE的中点,连结DF,CF.
(1)如图①,当点D在AB上,点E在AC上,请直接写出此时线段DF,CF的数量关系和位置关系.
(2)如图②,在(1)的条件下将△ADE绕点A顺时针旋转45°,请你判断此时(1)中的结论是否仍然成立,并证明你的判断.
(3)如图③,在(1)的条件下将△ADE绕点A顺时针旋转90°,若AD=1,AC=![]() ,求此时线段CF的长(直接写出结果).
,求此时线段CF的长(直接写出结果).
【答案】(1) DF=CF,DF⊥CF;(2)(1)中的结论仍然成立,证明见解析;(3)CF=![]() .
.
【解析】
(1)根据“直角三角形斜边上的中线等于斜边的一半”可知DF=CF,根据∠DFE=2∠DBF,∠CFE=2∠CBF,得到∠EFD+∠EFC=2∠ABC=90°,DF⊥CF.
(2)延长DF交BC于点G,先证明△DEF≌△GBF,得到DE=GB,DF=GF,根据AD=DE,AB=BC,得到DC=GC又因为∠ACB=90°,所以DF=CF且DF⊥CF.
(3)延长DF交BA于点H,先证明△DEF≌△HBF,得到DE=BH,根据旋转条件可以△ADH为直角三角形,由△ABC和△ADE是等腰直角三角形,AC=2![]() ,可以求出AB的值,进而可以根据勾股定理可以求出DH,再求出DF,求出得CF的值.
,可以求出AB的值,进而可以根据勾股定理可以求出DH,再求出DF,求出得CF的值.
(1) DF=CF. DF⊥CF.
(2)(1)中的结论仍然成立.证明如下:
如解图①,延长DF交BC于点G.
∵∠ADE=∠ACB=90°,∴DE∥BC,
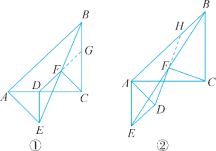
∴∠DEF=∠GBF,∠EDF=∠BGF.
∵F为BE的中点,∴EF=BF,
∴△DEF≌△GBF(AAS),
∴DE=GB,DF=GF.
∵AD=DE,∴AD=GB.
∵AC=BC,∴AC-AD=BC-GB,即DC=GC.
∵∠ACB=90°,∴△DCG是等腰直角三角形.
∵DF=GF,∴DF=CF,DF⊥CF.
(3)CF=![]() .
.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=kx2﹣7x﹣7的图象与x轴没有交点,则k的取值范围为( )
A.k>﹣ ![]()
B.k≥﹣ ![]() 且k≠0
且k≠0
C.k<﹣ ![]()
D.k>﹣ ![]() 且k≠0
且k≠0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据条件求二次函数的解析式
(1)二次函数y=ax2+bx+c的对称轴为x=3,最小值为﹣2,且过(0,1)点.
(2)抛物线过(﹣1,0),(3,0),(1,﹣5)三点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,△ABC各顶点都在格点上,点A,C的坐标分别为(﹣5,1)、(﹣1,4),结合所给的平面直角坐标系解答下列问题: 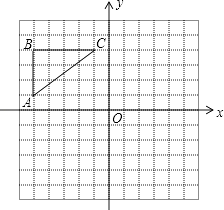
(1)①画出△ABC关于y轴对称的△A1B1C1;
②画出△ABC关于原点O对称的△A2B2C2;
(2)点C1的坐标是;点C2的坐标是;
(3)试判断:△A1B1C1与△A2B2C2是否关于x轴对称?(只需写出判断结果) .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=﹣ ![]() +bx+c的图象经过A(2,0)、B(0,﹣6)两点.
+bx+c的图象经过A(2,0)、B(0,﹣6)两点.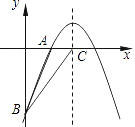
(1)求这个二次函数的解析式;
(2)设该二次函数的对称轴与x轴交于点C,连接BA,BC,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠A,∠B,∠C的对边分别记为![]() ,
,![]() ,
,![]() ,由下列条件不能判定△ABC为直角三角形的是( ).
,由下列条件不能判定△ABC为直角三角形的是( ).
A.∠A+∠B=∠C
B.∠A∶∠B∶∠C =1∶2∶3
C.![]()
D.![]() ∶
∶![]() ∶
∶![]() =3∶4∶6
=3∶4∶6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com