
| A. | 3-$\sqrt{6}$或1+$\sqrt{6}$ | B. | 3-$\sqrt{6}$或3+$\sqrt{6}$ | C. | 3+$\sqrt{6}$或1-$\sqrt{6}$ | D. | 1-$\sqrt{6}$或1+$\sqrt{6}$ |
分析 由解析式可知该函数在x=h时取得最小值1、x<h时,y随x的增大而增大、当x>h时,y随x的增大而减小,根据1≤x≤3时,函数的最小值为-5可分如下两种情况:①若h<1≤x≤3,x=1时,y取得最小值-5;②若1≤x≤3<h,当x=3时,y取得最小值-5,分别列出关于h的方程求解即可.
解答 解:∵当x<h时,y随x的增大而增大,当x>h时,y随x的增大而减小,
∴①若h<1≤x≤3,x=1时,y取得最小值-5,
可得:-(1-h)2+1=-5,
解得:h=1-$\sqrt{6}$或h=1+$\sqrt{6}$(舍);
②若1≤x≤3<h,当x=3时,y取得最小值-5,
可得:-(3-h)2+1=-5,
解得:h=3+$\sqrt{6}$或h=3-$\sqrt{6}$(舍).
综上,h的值为1-$\sqrt{6}$或3+$\sqrt{6}$,
故选:C.
点评 本题主要考查二次函数的性质和最值,根据二次函数的性质和最值分类讨论是解题的关键.


 名师点拨卷系列答案
名师点拨卷系列答案科目:初中数学 来源: 题型:解答题
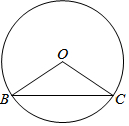 在⊙O中,己知弦BC所对的圆周角∠BAC与圆心角∠BOC互补.
在⊙O中,己知弦BC所对的圆周角∠BAC与圆心角∠BOC互补.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1cm,2cm,3.5cm | B. | 3cm,4cm,6cm | C. | 4cm,5cm,9cm | D. | 3cm,3cm,6cm |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
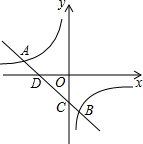 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于A(-3,1),B(2,n)两点,直线AB分别交x轴、y轴于D,C两点.
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于A(-3,1),B(2,n)两点,直线AB分别交x轴、y轴于D,C两点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,正方形ABCD的边长为1,点P为BC上任意一点(可以与B点或C重合),分别过B,C,D作射线AP的垂线,垂足分别是B',C',D',则BB'+CC'+DD'的最大值与最小值的和为2+$\sqrt{2}$.
如图,正方形ABCD的边长为1,点P为BC上任意一点(可以与B点或C重合),分别过B,C,D作射线AP的垂线,垂足分别是B',C',D',则BB'+CC'+DD'的最大值与最小值的和为2+$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
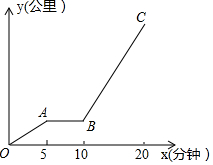 李狗蛋从家出发坐公交车去上学,他要先走到公交车站等公交车.他离家的距离y(米)与经过的时间x(分钟)的关系折线如图所示,已知狗蛋每分钟能走0.1公里,公交车的速度为0.4公里/分钟.
李狗蛋从家出发坐公交车去上学,他要先走到公交车站等公交车.他离家的距离y(米)与经过的时间x(分钟)的关系折线如图所示,已知狗蛋每分钟能走0.1公里,公交车的速度为0.4公里/分钟.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com