
【题目】如图,在△ABC中,∠C=90°,AC=8,BC=6,点D是AB的中点,点E在AC上,将△ADE沿DE翻折,使点A落在点A′处,当A′D与△ABC的一边平行时,A′B=____________.

【答案】![]() 或
或![]()
【解析】
根据题意,先求出AB的长度,由折叠后,A′D与△ABC的一边平行时,可分为两种情况进行①当![]() ∥AC时;②当
∥AC时;②当![]() ∥BC时;利用折叠的性质,矩形的性质,中位线定理,以及勾股定理,分别求出两种情况
∥BC时;利用折叠的性质,矩形的性质,中位线定理,以及勾股定理,分别求出两种情况![]() 的长度,即可得到答案.
的长度,即可得到答案.
解:在△ABC中,∠C=90°,AC=8,BC=6,
由勾股定理,得:![]() ,
,
∵点D是AB的中点,
∴AD=BD=5;
①当![]() ∥AC时,如图:
∥AC时,如图:
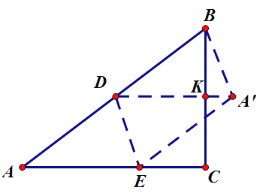
由折叠的性质,得:![]() ,
,
∵![]() ∥AC,点D是AB的中点,
∥AC,点D是AB的中点,
∴点K是BC的中点,
∴![]() ,
,![]() ,
,
∴![]() ,
,
在Rt△![]() 中,由勾股定理,得:
中,由勾股定理,得:
![]() ;
;
②当![]() ∥BC时,如图:过
∥BC时,如图:过![]() 作
作![]() ⊥BC于点G.
⊥BC于点G.
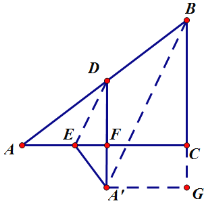
由折叠的性质,得![]() ,
,
∵![]() ∥BC,点D是AB的中点,
∥BC,点D是AB的中点,
∴点F是AC的中点,
∴![]() ,
,![]() ,
,
∴![]() ,
,
易得四边形![]() 是矩形,
是矩形,
∴![]() ,
,![]() ,
,
在Rt△![]() 中,由勾股定理得:
中,由勾股定理得:
![]() .
.
故答案为:![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】在解决数学问题时,我们常常从特殊入手,猜想结论,并尝试发现解决问题的策略与方法.
(问题提出)
求证:如果一个定圆的内接四边形对角线互相垂直,那么这个四边形的对边的平方和是一个定值.
(从特殊入手)
我们不妨设定圆O的半径是R,⊙O的内接四边形ABCD中,AC⊥BD.
请你在图①中补全特殊殊位置时的图形,并借助于所画图形探究问题的结论.

(问题解决)
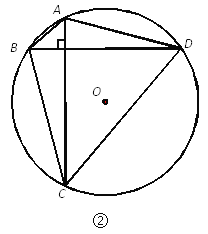
已知:如图②,定圆⊙O的半径是R,四边形ABCD是⊙O的内接四边形, AC⊥BD.
求证: .
证明:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=45°,点M,N在边OA上,OM=x,ON=x+4,点P是边OB上的点.若使点P,M,N构成等腰三角形的点P恰好有三个,则x的值是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在⊙O上.
(1)求∠AED的度数;
(2)若⊙O的半径为2,则![]() 的长为多少?
的长为多少?
(3)连接OD,OE,当∠DOE=90°时,AE恰好是⊙O的内接正n边形的一边,求n的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y=y1+y2,y1与x+1成正比例,y2与x+1成反比例,当x=0时,y=﹣5;当x=2时,y=﹣7.
(1)求y与x的函数关系式;
(2)当x=5时,求y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
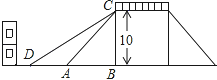
【题目】如图是一座人行天桥的示意图,天桥的高度是10米,CB⊥DB,坡面AC的倾斜角为45°.为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的坡度为i=![]() :3.若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据:
:3.若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,割线PCD交⊙O于C、D,∠PAE=∠PDA.
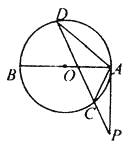
(1)求证:PA是⊙O的切线;
(2)若PA=6,CD=3PC,求PD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
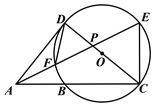
【题目】如图,△ACE,△ACD均为直角三角形,∠ACE=90°,∠ADC=90°,AE与CD相交于点P,以CD为直径的⊙O恰好经过点E,并与AC,AE分别交于点B和点F.
(1)求证:∠ADF=∠EAC.
(2)若PC=![]() PA,PF=1,求AF的长.
PA,PF=1,求AF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com