
如图.直线l过A(4,0)和B(0,4)两点,它与二次函数y=ax2的图象在第一象限内相交于P点,且△AOP的面积为![]() ,求二次函数的解析式.
,求二次函数的解析式.

|
解:设直线l为y=kx+b(k≠0),P的坐标为(xP,yP). ∵直线l过A(4,0)和B(0,4), ∴ ∴直线l的解析式为y=-x+4. ∵S△AOP= ∴|yP|= ∵点P在第一象限, ∴yP>0, ∴yP= ∵点P在l上, ∴ 得xP= 又∵点P在抛物线y=ax2上. ∴ ∴二次函数解析式为y= 思路点拨:本题的关键是求点P的坐标,根据:①点P在l上;②点P在抛物线y=ax2上;③点P的纵坐标是△AOP底边OA上的高.可求得点P的坐标,若灵活运用这三个条件则可使运算简便,不然就会给计算带来很多麻烦.其思考顺序应为:先由三角形面积列式求点P的纵坐标,然后把它代入直线l的方程,求得点P的横纵标,最后把点P的坐标代入y=ax2,得到关于a的方程,从而求得a. 评注:本例属于一次函数与最简单的二次函数y=ax2的综合题,要能确定一般的一次函数解析式,必须有两对对应值,确定y=ax2型的解析式,需要与它有关的一对对应值,若这些条件不能直接得到,那就得充分挖掘题中条件来满足解题需要. |


科目:初中数学 来源: 题型:
 如图,直线EF过平行四边形ABCD对角线的交点O,分别交AB、CD于E、F,若平行四边形的面积是12,则△AOE与△DOF的面积和为( )
如图,直线EF过平行四边形ABCD对角线的交点O,分别交AB、CD于E、F,若平行四边形的面积是12,则△AOE与△DOF的面积和为( )| A、4 | B、3 | C、2 | D、6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| m |
| x |
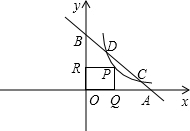 D两点,P为双曲线y=
D两点,P为双曲线y=| m |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
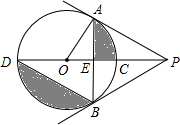 如图,直线PCD过圆心O,PA、PB分别切⊙O于A、B,∠APB=60°,PA=4,AB与PD相交于E.
如图,直线PCD过圆心O,PA、PB分别切⊙O于A、B,∠APB=60°,PA=4,AB与PD相交于E.查看答案和解析>>
科目:初中数学 来源: 题型:
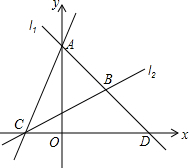 如图,直线l1过点A(0,4)、D(4,0)两点,直线l2:y=
如图,直线l1过点A(0,4)、D(4,0)两点,直线l2:y=| 1 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com