
分析 (1)将A(-3,0)、B(1,0),代入y=ax2+bx+3求出抛物线解析式,再求出顶点坐标即可;
(2)首先求出直线CA的解析式为y=k1x+b1,再利用联立两函数解析式即可得出交点坐标,再利用若点P在对称轴左侧(如图②),只能是△PCQ∽△ACH,得∠PCQ=∠ACH得出答案即可.
解答 解:(1)将A(-3,0)、B(1,0),代入y=ax2+bx+3,
得:$\left\{{\begin{array}{l}{9a-3b+3=0}\\{a+b+3=0}\end{array}}\right.$
解得:$\left\{{\begin{array}{l}{a=-1}\\{b=-2}\end{array}}\right.$
抛物线的解析式为:y=-x2-2x+3,
顶点C的坐标为(-1,4).
(2)①若点P在对称轴右侧(如图①),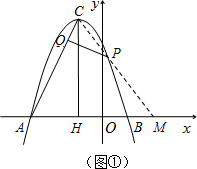
只能是△PCQ∽△CAH,得∠QCP=∠CAH.
延长CP交x轴于M,∴AM=CM,∴AM2=CM2.
设M(m,0),则( m+3)2=42+(m+1)2,∴m=2,即M(2,0).
设直线CM的解析式为y=k1x+b1,
则$\left\{\begin{array}{l}-{k_1}+{b_1}=4\\ 2{k_1}+{b_1}=0\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{1}=-\frac{4}{3}}\\{{b}_{1}=\frac{8}{3}}\end{array}\right.$,
∴直线CM的解析式$y=-\frac{4}{3}x+\frac{8}{3}$,
联立$\left\{\begin{array}{l}{y=-\frac{4}{3}x+\frac{8}{3}}\\{y=-{x}^{2}-2x+3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=\frac{1}{3}}\\{y=\frac{20}{9}}\end{array}\right.$或$\left\{\begin{array}{l}{x=-1}\\{y=4}\end{array}\right.$(舍去).
∴$P(\frac{1}{3},\frac{20}{9})$.
②若点P在对称轴左侧(如图②),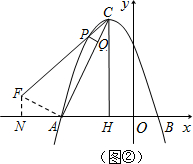
只能是△PCQ∽△ACH,得∠PCQ=∠ACH.
过A作CA的垂线交PC于点F,作FN⊥x轴于点N.
由△CFA∽△CAH得$\frac{CA}{AF}=\frac{CH}{AH}=2$,
由△FNA∽△AHC得$\frac{FN}{AH}=\frac{NA}{HC}=\frac{AF}{CA}=\frac{1}{2}$.
∴AN=2,FN=1,点F坐标为(-5,1).
设直线CF的解析式为y=k2x+b2,则$\left\{\begin{array}{l}-{k_2}+{b_2}=4\\-5{k_2}+{b_2}=1\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{2}=\frac{3}{4}}\\{{b}_{2}=\frac{19}{4}}\end{array}\right.$.
∴直线CF的解析式$y=\frac{3}{4}x+\frac{19}{4}$,
联立$\left\{\begin{array}{l}{y=\frac{3}{4}x+\frac{19}{4}}\\{y=-{x}^{2}-2x+3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=-\frac{7}{4}}\\{y=\frac{55}{16}}\end{array}\right.$或$\left\{\begin{array}{l}{x=-1}\\{y=4}\end{array}\right.$(舍去).
∴$P(-\frac{7}{4},\frac{55}{16})$.
∴满足条件的点P坐标为$(\frac{1}{3},\frac{20}{9})$或$(-\frac{7}{4},\frac{55}{16})$.
点评 此题主要考查了二次函数的综合应用以及相似三角形的应用,二次函数的综合应用是初中阶段的重点题型,解决本题的关键是利用数形结合的思想解决问题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
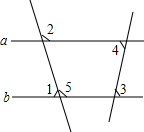 如图,已知∠1=80°,∠2=100°,∠3=85°,求∠4的度数.
如图,已知∠1=80°,∠2=100°,∠3=85°,求∠4的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
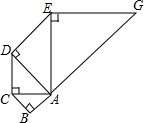 如图,以1为腰长画等腰直角三角形Rt△ACB,又以Rt△ACB的斜边AC长为直角边画第2个等腰直角三角形Rt△ADC,再以Rt△ADC的斜边AD长为直角边画第3个等腰直角三角形Rt△ADE,依此类推,则第2015个等腰直角三角形的斜边长为${(\sqrt{2})}^{2015}$.
如图,以1为腰长画等腰直角三角形Rt△ACB,又以Rt△ACB的斜边AC长为直角边画第2个等腰直角三角形Rt△ADC,再以Rt△ADC的斜边AD长为直角边画第3个等腰直角三角形Rt△ADE,依此类推,则第2015个等腰直角三角形的斜边长为${(\sqrt{2})}^{2015}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com