
【题目】为了加强学生的交通安全意识,某中学和交警大队联合举行了“我当一日小交警”活动,星期天选派部分学生到交通路口值勤,协助交通警察维护交通秩序.若每一个路口安排4人,那么还剩下78人;若每个路口安排8人,那么最后一个路口不足8人,但不少于4人.求这个中学共选派值勤学生多少人?共有多少个交通路口安排值勤?
 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,点O在AB上,经过点A的⊙O与BC相切于点D,与AC,AB分别相交于点E,F,连接AD与EF相交于点G.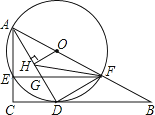
(1)求证:AD平分∠CAB;
(2)若OH⊥AD于点H,FH平分∠AFE,DG=1.
①试判断DF与DH的数量关系,并说明理由;
②求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC经过一次平移到△DFE的位置,请回答下列问题:

(1)点C的对应点是点__________,∠D=__________,BC=__________;
(2)连接CE,那么平移的方向就是__________的方向,平移的距离就是线段__________的长度;
(3)连接AD,BF,BE,与线段CE相等的线段有__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动.已知点A的速度是1单位长度/秒,点B的速度是点A的速度的4倍(速度单位:单位长度/秒).
(1)求请在数轴上标出A、B两点从原点出发运动3秒时的位置;
![]()
(2)若A、B两点在(1)中的位置,数轴上是否存在一点P到点A,点B的距离之和为16,并求出此时点P表示的数;若不存在,请说明理由.
(3)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动时,另一点C同时从B点位置出发向A点运动,当遇到A点后,立即返回向B点运动,遇到B点后又立即返回向A点运动,如此往返,直到B点追上A点时,C点立即停止运动.若点C一直以10单位长度/秒的速度匀速运动,那么点C从开始运动到停止运动,行驶的路程是多少个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在综合实践课上,小聪所在小组要测量一条河的宽度,如图,河岸EF∥MN,小聪在河岸MN上点A处用测角仪测得河对岸小树C位于东北方向,然后沿河岸走了30米,到达B处,测得河对岸电线杆D位于北偏东30°方向,此时,其他同学测得CD=10米.请根据这些数据求出河的宽度为米.(结果保留根号)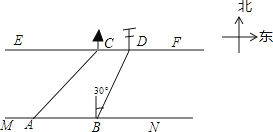
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料阅读:若一个整数能表示成a2+b2(a、b是正整数)的形式,则称这个数为“完美数”.例如:因为13=32+22,所以13是“完美数”;再如:因为a2+2ab+2b2=(a+b)2+b2(a、b是正整数),所以a2+2ab+2b2也是“完美数”.
(1)请你写出一个大于20小于30的“完美数”,并判断53是否为“完美数”;
(2)试判断(x2+9y2)·(4y2+x2)(x、y是正整数)是否为“完美数”,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一茶叶专卖店经销某种品牌的茶叶,该茶叶的成本价是80元/kg,销售单价不低于120元/kg.且不高于180元/kg,经销一段时间后得到如下数据:
销售单价x(元/kg) | 120 | 130 | … | 180 |
每天销量y(kg) | 100 | 95 | … | 70 |
设y与x的关系是我们所学过的某一种函数关系.
(1)直接写出y与x的函数关系式,并指出自变量x的取值范围;
(2)当销售单价为多少时,销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某研究性学习小组在探究矩形的折纸问题时,将一块直角三角板的直角顶点绕着矩形ABCD(AB<BC)的对角线交点O旋转(如图①→②→③),图中M、N分别为直角三角板的直角边与矩形ABCD的边CD、BC的交点.
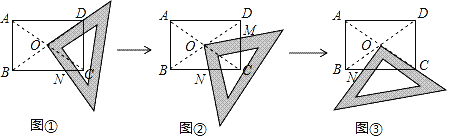
(1)该学习小组中一名成员意外地发现:在图①(三角板的一直角边与OD重合)中,BN2=CD2+CN2;在图③(三角板的一直角边与OC重合)中,CN2=BN2+CD2.请你对这名成员在图①和图③中发现的结论选择其一说明理由.
(2)试探究图②中BN、CN、CM、DM这四条线段之间的关系,写出你的结论,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD为△ABC的中线,BE为△ABD的中线.
(1)在△BED中作BD边上的高,垂足为F;
(2)若△ABC的面积为40,BD=5,则△BDE中BD边上的高为多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com