
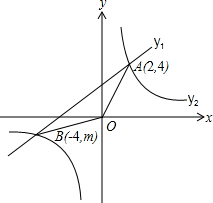
如图,已知一次函数 (m为常数)的图象与反比例函数
(m为常数)的图象与反比例函数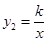 (k为常数,
(k为常数,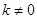 )的图象相交于点 A(1,3).
)的图象相交于点 A(1,3).
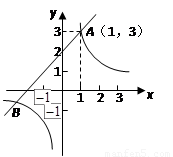
(1)求这两个函数的解析式及其图象的另一交点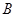 的坐标;
的坐标;
(2)观察图象,写出使函数值 的自变量
的自变量 的取值范围.
的取值范围.
(1)一次函数解析式为:y1=x+2,B(﹣3,﹣1);
(2)根据图象得:函数值y1≥y2的自变量x的取值范围是:x≥1或﹣3≤x<0.
【解析】
试题分析:(1)利用待定系数法把 A(1,3)代入一次函数y1=x+m与反比例函数 中,可解出m、k的值,进而可得解析式,求B点坐标,就是把两函数解析式联立,求出x、y的值;
中,可解出m、k的值,进而可得解析式,求B点坐标,就是把两函数解析式联立,求出x、y的值;
(2)根据函数图象可以直接写出答案.
试题解析:(1)∵一次函数y1=x+m(m为常数)的图象与反比例函数 (k为常数,k≠0)的图象相交于点 A(1,3),
(k为常数,k≠0)的图象相交于点 A(1,3),
∴3=1+m,k=1×3,
∴m=2,k=3,
∴一次函数解析式为:y1=x+2,
反比例函数解析式为:y2= ,
,
由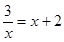 ,
,
解得:x1=﹣3,x2=1,
当x1=﹣3时,y1=﹣1,
x2=1时,y1=3,
∴两个函数的交点坐标是:A(1,3)和B(﹣3,﹣1)
∴B(﹣3,﹣1);
(2)根据图象得:函数值y1≥y2的自变量x的取值范围是:x≥1或﹣3≤x<0.
考点:反比例函数解析式,一次函数解析式,反比例函数的性质.


科目:初中数学 来源: 题型:
| a | x |
 B(-4,m)两点.
B(-4,m)两点.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知一次函数y=kx+b的图象与反比例函数y=-
如图,已知一次函数y=kx+b的图象与反比例函数y=-| 8 | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•新疆)如图,已知一次函数y1=kx+b与反比例函数y2=
(2013•新疆)如图,已知一次函数y1=kx+b与反比例函数y2=| m | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知一次函数y=k1x+b经过A、B两点,将点A向上平移1个单位后刚好在反比例函数y=
如图,已知一次函数y=k1x+b经过A、B两点,将点A向上平移1个单位后刚好在反比例函数y=| k2 | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知一次函数y=kx+b的图象交反比例函数y=
如图,已知一次函数y=kx+b的图象交反比例函数y=| 4-2m |
| x |
| BC |
| AB |
| 1 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com