
【题目】已知,![]() 是
是![]() 的直径,
的直径,![]() 、
、![]() 是
是![]() 上的点,连接
上的点,连接![]() 、
、![]() 、
、![]() ,
,![]() 是
是![]() 的切线,过点
的切线,过点![]() 作
作![]() .
.
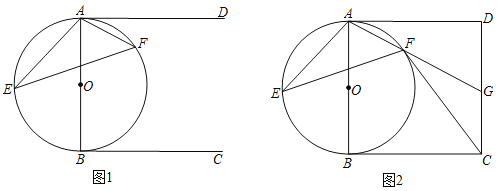
(1)如图1,求证:![]() ;
;
(2)如图2,若![]() ,连接
,连接![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,若
,若![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)![]()
![]()
【解析】
(1)如图1,连接BF,根据切线的性质得到∠ABC=90°,根据圆周角定理得到∠AFB=90°,推出∠ABF=∠DAF,等量代换即可得到结论;
(2)如图2,连接OF,OC,根据全等三角形的性质得到∠OFC=∠ABC=90°,∠BOC=∠FOC,推出∠BAG=∠BOC,得到四边形ABCD是正方形,于是得到AB=CD,∠D=90°,AB∥CD,根据全等三角形的性质得到AD=BC=4,DG=BO=2,根据勾股定理得到AG=![]() .
.
(1)证明:如图1,连接BF,
∵AB是⊙O的直径,BC是⊙O的切线,
∴∠ABC=90°,
∵AD∥BC,
∴∠DAB=90°,
∴∠DAF+∠BAF=90°,
∵AB是⊙O的直径,
∴∠AFB=90°,
∴∠ABF+∠BAF=90°,
∴∠ABF=∠DAF,
∵∠AEF=∠ABF,
∴∠AEF=∠DAF;
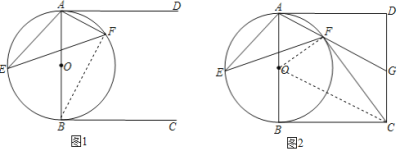
(2)解:如图2,连接OF,OC,
在△CBO与△CFO中,
OB=OF,
BC=FC,
OC=OC,
∴△CBO≌△CFO(SSS),
∴∠OFC=∠ABC=90°,∠BOC=∠FOC,
∵OA=OF,
∴∠OAF=∠OFA,
∵∠OAF=![]() ,∠BOC=
,∠BOC=![]() ,
,
∴∠OAF=∠BOC,
∵AD=BC,AD∥BC,
∴四边形ABCD是平行四边形,
∵AB=BC,∠ABC=90°,
∴四边形ABCD是正方形,
∴AB=CD,∠D=90°,AB∥CD,
∴∠BAG=∠DGA=∠BOC,
在△ADG与△CBO中,
∠ABC=∠D,
∠BOC=∠AGD,
BC=AD,
∴△ADG≌△CBO(AAS),
∴AD=BC=4,DG=BO=2,
∴AG=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=90°,AB=2cm,AC=4cm.动点P从点A出发,沿AB方向以1cm/s的速度向点B运动,动点Q从点B同时出发,沿BA方向以1cm/s的速度向点A运动.当点P到达点B时,P,Q两点同时停止运动,以AP为一边向上作正方形APDE,过点Q作QF∥BC,交AC于点F.设点P的运动时间为ts,正方形和梯形重合部分的面积为Scm2.
(1)当t= _________ s时,点P与点Q重合;
(2)当t= _________ s时,点D在QF上;
(3)当点P在Q,B两点之间(不包括Q,B两点)时,求S与t之间的函数关系式.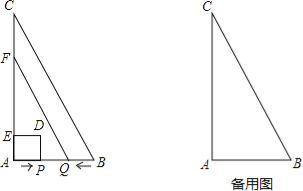
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为A(0,a),B(b,a),且a,b满足(a﹣3)2+|b﹣6|=0,现同时将点A,B分别向下平移3个单位,再向左平移2个单位,分别得到点A,B的对应点C,D,连接AC,BD,AB.

(1)求点C,D的坐标及四边形ABDC的面积S四边形ABCD;
(2)在y轴上是否存在一点M,连接MC,MD,使S△MCD=![]() S四边形ABCD?若存在这样一点,求出点M的坐标,若不存在,试说明理由;
S四边形ABCD?若存在这样一点,求出点M的坐标,若不存在,试说明理由;
(3)点P是直线BD上的一个动点,连接PA,PO,当点P在BD上移动时(不与B,D重合),直接写出∠BAP,∠DOP,∠APO之间满足的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴的一个交点为
轴的一个交点为![]() ,与
,与![]() 轴的交点
轴的交点![]() 在点
在点![]() 与点
与点![]() 之间(包含端点),顶点
之间(包含端点),顶点![]() 的坐标为
的坐标为![]() 。则下列结论:①
。则下列结论:①![]() ;②
;②![]() ;③对于任意实数
;③对于任意实数![]() ,
,![]() 总成立;④关于
总成立;④关于![]() 的方程
的方程![]() 没有实数根。其中结论正确的个数为()
没有实数根。其中结论正确的个数为()

A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
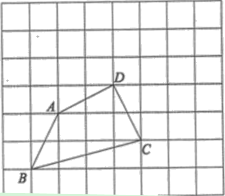
【题目】如图,在由边长都为1的小正方形组成的网格中,点![]() 均为格点.
均为格点.
(Ⅰ)线段![]() 的长度等于______;
的长度等于______;
(Ⅱ)若![]() 为线段
为线段![]() 上一点,且满足
上一点,且满足![]() ,请你借助无刻度直尺在给定的网格中面出满足条件的线段
,请你借助无刻度直尺在给定的网格中面出满足条件的线段![]() ,并简要说明你是怎么画出点
,并简要说明你是怎么画出点![]() ______________________.
______________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为纪念建国70周年,某校举行班级歌咏比赛,歌曲有:《我爱你,中国》,《歌唱祖国》,《我和我的祖国》(分别用字母A,B,C依次表示这三首歌曲).比赛时,将A,B,C这三个字母分别写在3张无差别不透明的卡片正面上,洗匀后正面向下放在桌面上,八(1)班班长先从中随机抽取一张卡片,放回后洗匀,再由八(2)班班长从中随机抽取一张卡片,进行歌咏比赛.
(1)八(1)班抽中歌曲《我和我的祖国》的概率是__________;
(2)试用画树状图或列表的方法表示所有可能的结果,并求出八(1)班和八(2)班抽中不同歌曲的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=x+m与双曲线y=![]() 相交于A(2,1),B两点.
相交于A(2,1),B两点.
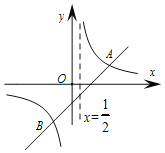
(1)求出一次函数与反比例函数的解析式,并求出B点坐标;
(2)若P为直线x=![]() 上一点,当△APB的面积为6时,请求出点P的坐标.
上一点,当△APB的面积为6时,请求出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com