Question

【题目】如图，在中，的垂直平分线交于点，交于点，且，的周长等于。

（1）求的长；

（2）若，并且，求证：。

Answer 1

【答案】（1）10；（2）证明见详解

【解析】

（1）根据线段垂直平分线上的点到线段两端点的距离相等可得AE=BE，然后求出△BCE的周长=AC+BC，再求解即可；

（2）根据等腰三角形两底角相等求出∠C=72°，根据线段垂直平分线上的点到线段两端点的距离相等可得AE=BE，根据等边对等角可得∠ABE=∠A，再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠BEC=72°，从而得到∠BEC=∠C，然后根据等角对等边求解．

解：如图：

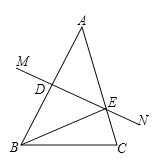
（1）∵AB的垂直平分线MN交AB于点D，:

∴AE=BE，

∴△BCE的周长=BE+CE+BC=AE+CE+BC=AC+BC，

∵AC=15cm，

∴BC=25-15=10cm；

（2）证明：∵∠A=36°，AB=AC，

∴∠C=（180°-∠A）=（180°-36°）=72°，

∵AB的垂直平分线MN交AB于点D，

∴AE=BE，

∴∠ABE=∠A，

由三角形的外角性质得，∠BEC=∠A+∠ABE=36°+36°=72°，

∴∠BEC=∠C，

∴BC=BE．