
 【实际情境】
【实际情境】
|
|
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 8 |
| 3 |
| 2 |
| 3 |
| 8 |
| 3 |
| 2 |
| 3 |
| 8 |
| 3 |
|
|
| 2 |
| 7 |
| 10 |
| 17 |
| 2 |
| 7 |
| 10 |
| 17 |


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
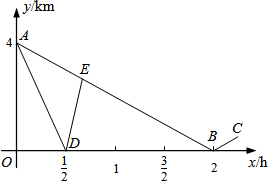
 已知:如图,在平面直角坐标系xOy中,点A(2
已知:如图,在平面直角坐标系xOy中,点A(2| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
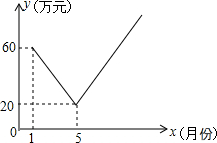 保护生态环境,实行“节能减排”的理念已深入人心.我市某工厂从2014年1月开始,进行机器设备更新,产业转型换代的改造,改造期间利润明显下降,从1月份利润60万元逐月等额下降,到5月份利润为20万元;5月底改造完成,从这时起,该厂每个月的利润都比上个月增加15万元.设第x个月的利润为y(万元),函数图象如图.
保护生态环境,实行“节能减排”的理念已深入人心.我市某工厂从2014年1月开始,进行机器设备更新,产业转型换代的改造,改造期间利润明显下降,从1月份利润60万元逐月等额下降,到5月份利润为20万元;5月底改造完成,从这时起,该厂每个月的利润都比上个月增加15万元.设第x个月的利润为y(万元),函数图象如图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com