
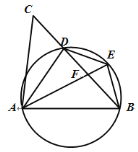
【题目】如图,D是△ABC的BC边上一点,连接AD,作△ABD的外接圆,将△ADC沿直线AD折叠,点C的对应点E落在圆上,连接AE,AE与BD相交于点F.
(1)求证:AE=AB;
(2)若E为弧BD的中点,试说明:DE2=EF·AE;
(3)在(2)的条件下,若cos∠ADB=![]() ,BE=2,求AF的长.
,BE=2,求AF的长.
【答案】(1)证明见解析;(2)证明见解析;(3) AF=3.
【解析】
(1)先根据翻折的性质和圆周角定理得出∠C=∠AED=∠ABC和AC=AE再推出AC=AB,从而得到AE=AB;
(2)根据E为弧BD的中点和圆周角定理得出∠DAE=∠EDB,然后证明△DEF∽△AED;
(3)作AH⊥BE,利用三角函数求出AE=4,利用(2)相似线段关系求出EF=1,从而得出:AF=3.
(1)由折叠的性质可知△ADE≌△ADC
∴∠AED=∠ACD,AE=AC,
∵∠ABD=∠AED,
∴∠ABD=∠ACD,
∴AB=AC,
∴AE=AB;
(2)∵E为弧BD的中点
∴∠DAE=∠EAB
∵∠EDB=∠EAB
∴∠DAE=∠EDB
∴△DEF∽△AED
∴![]()
∴![]()
(3)过A作AH⊥BE于点H

∵AB=AE,BE=2,
∴BH=EH=1,
∵∠ABE=∠AEB=∠ADB,![]() ,
,
∴![]() ,
,
∴![]() .
.
∴AC=AB=4
∵E为弧BD的中点
∴DE=EB=2
根据(2)中的结论![]()
可得:![]()
∴EF=1
∴AF=AE-EF=3


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
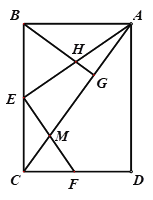
【题目】 如图,![]() 是矩形
是矩形![]() 的边
的边![]() 上的一点,AC是其对角线,连接AE,过点E作
上的一点,AC是其对角线,连接AE,过点E作![]() 交
交![]() 于点
于点![]() ,
, ![]() 交DC于点F,过点B作
交DC于点F,过点B作![]() 于点G,
于点G,![]() 交AE于点H.
交AE于点H.
(1)求证:![]() ∽
∽![]() ;
;
(2)求证:![]() ;
;
(3)若E是BC的中点,![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图C是线段BD上一点,分别以BC、CD为边在BD同侧作等边△ABC和等边△CDE,AD交CE于F,BE交AC于G,则图中可通过旋转而相互得到的三角形对数有( )

A.1对B.2对C.3对D.4对
查看答案和解析>>
科目:初中数学 来源: 题型:
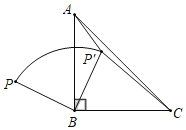
【题目】如图,点P是等腰Rt△ABC外一点,把线段BP绕点B顺时针旋转90°得到线段BP',已知∠AP'B=135°,P'A:P'C=1:3,则P'A:PB=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
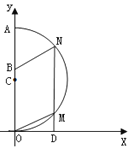
【题目】如图,在平面直角坐标系中,平行四边形BOMN的一边延长线交x轴于点D,OB=18,OD=12,点C为线段BO上一点,以C点为圆心,CO为半径的圆过M、N两点,且与y轴交于点A,则OA长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的.连接BE、CF相交于点D.
(1)求证:BE=CF.
(2)当四边形ACDE为菱形时,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场在“五一”促销活动中规定,顾客每消费100元就能获得一次中奖机会.为了活跃气氛.设计了两个抽奖方案:
方案一:转动转盘![]() 一次,转出红色可领取一份奖品;
一次,转出红色可领取一份奖品;
方案二:转动转盘![]() 两次,两次都转出红色可领取一份奖品.(两个转盘都被平均分成3份)
两次,两次都转出红色可领取一份奖品.(两个转盘都被平均分成3份)
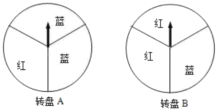
(1)若转动一次![]() 转盘,求领取一份奖品的概率;
转盘,求领取一份奖品的概率;
(2)如果你获得一次抽奖机会,你会选择哪个方案?请采用列表法或树状图说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有长为24m的篱笆,围成中间隔有一道篱笆的长方形的花圃,且花圃的长可借用一段墙体(墙体的最大可用长度a=10m).

(1)如果所围成的花圃的面积为45m2,试求宽AB的长;
(2)按题目的设计要求,能围成面积比45m2更大的花圃吗?如果能,请求出最大面积,并说明围法;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平面直角坐标系xOy中,抛物线y=ax2+2x+c与x轴交于点A(﹣1,0)和点B,与y轴相交于点C(0,3),抛物线的对称轴为直线![]() .
.
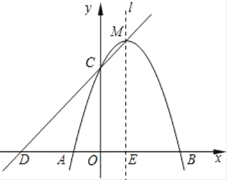
(1)求这条抛物线的关系式,并写出其对称轴和顶点M的坐标;
(2)如果直线y=kx+b经过C、M两点,且与x轴交于点D,点C关于直线![]() 的对称点为N,试证明四边形CDAN是平行四边形;
的对称点为N,试证明四边形CDAN是平行四边形;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com