
【题目】如图,锐角三角形ABC中,O为三条边的垂直平分线的交点,I为三个角的平分线的交点,若∠BOC的度为x,∠BIC的度数为y,则x、y之间的数量关系是( )
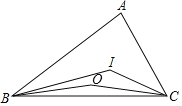
A.x+y=90°B.x﹣2y=90°C.x+180°=2yD.4y﹣x=360°
【答案】D
【解析】
根据线段垂直平分线的性质可得x=2∠A,根据角平分线的定义可得y=90°+![]() A,整理即可得到结论.
A,整理即可得到结论.
解:作OD⊥BC与点D,作OE⊥AB与点E,作OF⊥AC与点F,连接OA,
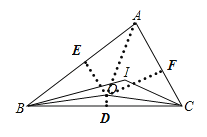
∵O为三条边的垂直平分线的交点,
∴OA=OB=OC,
∴∠OBC=∠OCB, ∠OAB=∠OBA, ∠OAC=∠OCA,
∵∠OBC+∠OCB+ ∠OAB+∠OBA+∠OAC+∠OCA=180°, ∠OBC+∠OCB=180°-x,
∴180°-x+2∠A=180°,
∴x=2∠A,
∵I为三个角的平分线的交点,
∴∠ABI=∠CBI, ∠ACI=∠BCI,
y=180°-(![]() ∠ABC+
∠ABC+![]() ∠ACB), ∠ABC+∠ACB=180°-∠A,
∠ACB), ∠ABC+∠ACB=180°-∠A,
∴y=90°+![]() A,
A,
∴y=90°+![]() x,
x,
∴4y﹣x=360°,
故选:D.


科目:初中数学 来源: 题型:
【题目】广州火车南站广场计划在广场内种植A,B两种花木共 6600棵,若A花木数量是B花木数量的2倍少600棵.
(1)A,B两种花木的数量分别是多少棵?
(2)如果园林处安排26人同时种植这两种花木,每人每天能种植A花木60棵或B花木40棵,应分别安排多少人种植A花木和B花木,才能确保同时完成各自的任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(4,3)是反比例函数y=![]() 在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y=
在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y=![]() 的图象于点P.
的图象于点P.
(1)求反比例函数y=![]() 的表达式;
的表达式;
(2)求点B的坐标;
(3)求△OAP的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列结论:![]() 平分弦的直径垂直于弦;
平分弦的直径垂直于弦;![]() 圆周角的度数等于圆心角的一半;
圆周角的度数等于圆心角的一半;![]() 等弧所对的圆周角相等;
等弧所对的圆周角相等;![]() 经过三点一定可以作一个圆;
经过三点一定可以作一个圆;![]() 三角形的外心到三边的距离相等;
三角形的外心到三边的距离相等;![]() 垂直于半径的直线是圆的切线.
垂直于半径的直线是圆的切线.
其中正确的个数为( )
A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠1=∠2,G为AD中点,延长BG交AC于E,F为AB上一点,且CF⊥AD于H,下列判断,①BG是△ABD中边AD上的中线;②AD既是△ABC中∠BAC的角平分线,也是△ABE中∠BAE的角平分线;③CH既是△ACD中AD边上的高线,也是△ACH中AH边上的高线,其中正确的个数是( )
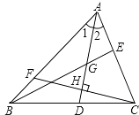
A.0B.1C.2D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的点坐标分别为A(2,3),B(1,1),C(2,1).
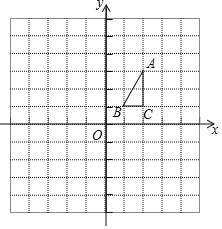
(1)画出△ABC关于x轴对称的△A1B1C1,并写出A1,B1,C1的坐标;
(2)直按写出△ABC关于直线m(直线m上各点的横坐标都为﹣1)对称的△A2B2C2的坐标:A2 ,B2 ,C2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象如图所示,
的图象如图所示,
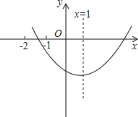
![]() 给出三个结论:①
给出三个结论:①![]() ;②
;②![]() ;③
;③![]() ,其中正确结论的序号是:________.
,其中正确结论的序号是:________.
![]() 给出三个结论:①
给出三个结论:①![]() ;②
;②![]() ;③
;③![]() ,其中正确结论的序号是:________.
,其中正确结论的序号是:________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com