
【题目】已知一次函数y1=kx+n(n<0)和反比例函数y2=![]() (m>0,x>0).
(m>0,x>0).
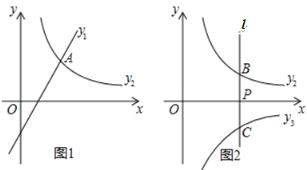
(1)如图1,若n=﹣2,且函数y1、y2的图象都经过点A(3,4).
①求m,k的值;
②直接写出当y1>y2时x的范围;
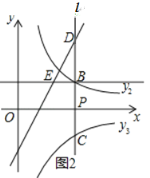
(2)如图2,过点P(1,0)作y轴的平行线l与函数y2的图象相交于点B,与反比例函数y3=![]() (x>0)的图象相交于点C.
(x>0)的图象相交于点C.
①若k=2,直线l与函数y1的图象相交点D.当点B、C、D中的一点到另外两点的距离相等时,求m﹣n的值;
②过点B作x轴的平行线与函数y1的图象相交于点E.当m﹣n的值取不大于1的任意实数时,点B、C间的距离与点B、E间的距离之和d始终是一个定值.求此时k的值及定值d.
【答案】(1)①m=12;k=2;②x>3;(2)①m﹣n=1或4或2;②k=1,d=1.
【解析】
(1)①将点A的坐标代入一次函数表达式即可得出k的值,将点A的坐标代入反比例函数表达式即可得出m的值;②由图象可以直接得出结果;
(2)①当x=1时,点D、B、C的坐标分别为(1,2+n)、(1,m)、(1,n),则BD=|2+n-m|,BC=m-n,DC=2+n-n=2,由BD=BC或BD=DC或BC=CD,即可求解;②先得出点E的坐标为![]() ,当点E在点B左侧时,d=BC+BE=m-n+
,当点E在点B左侧时,d=BC+BE=m-n+![]() =1+(m-n)(1-
=1+(m-n)(1-![]() ),由1-
),由1-![]() =0即可求解;当点E在点B右侧时,同理BC+BE=(m﹣n)(1+
=0即可求解;当点E在点B右侧时,同理BC+BE=(m﹣n)(1+![]() )﹣1,不合题意舍去.
)﹣1,不合题意舍去.
解:(1)①当n=-2时,一次函数为y1=kx-2,
将点A的坐标(3,4)代入一次函数表达式得,4=3k-2,解得k=2,
将点A的坐标(3,4)代入反比例函数y2=![]() 得,m=3×4=12;
得,m=3×4=12;
②由图象可以看出x>3时,y1>y2;
(2)①由k=2,则y1=2x+n,
当x=1时,点D、B、C的坐标分别为(1,2+n)、(1,m)、(1,n),
则BD=|2+n﹣m|,BC=m﹣n,DC=2+n﹣n=2,
则BD=BC或BD=DC或BC=CD,
即:|2+n﹣m|=m﹣n或|2+n﹣m|=2或m﹣n=2,
即:m﹣n=1或0或2或4,
当m﹣n=0时,m=n与题意不符,
点D不能在C的下方,即BC=CD也不存在,n+2>n,
当B、D重合时,m﹣n=2成立,
故m﹣n=1或4或2;
②∵点E的纵坐标与点B的纵坐标相等为m,
y1=kx+n中令y1=m得,点E的横坐标为![]() ,
,
当点E在点B左侧时,
d=BC+BE=m﹣n+(1﹣![]() )=1+(m﹣n)(1﹣
)=1+(m﹣n)(1﹣![]() ),
),
m﹣n的值取不大于1的任意数时,d始终是一个定值,
当1﹣![]() =0时,此时k=1,从而d=1.
=0时,此时k=1,从而d=1.
当点E在点B右侧时,
同理d=BC+BE=(m﹣n)(1+![]() )﹣1,
)﹣1,
当1+![]() =0,k=﹣1时,(不合题意舍去)
=0,k=﹣1时,(不合题意舍去)
故k=1,d=1.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC的平分线AD与边BC的垂直平分线ED相交于点D,过点D作DF⊥AC交AC延长线于点F,若AB=8,AC=4,则CF的长为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,反比例函数y=![]() (x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点,△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )
(x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点,△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )

A. 6![]() B. 10 C. 2
B. 10 C. 2![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线AC⊥AB,O为AC的中点,经过点O的直线交AD于E,交BC于F,连结AF、CE,现在添加一个适当的条件,使四边形AFCE是菱形,下列条件:①OE=OA;②EF⊥AC;③AF平分∠BAC;④E为AD中点.正确的有( )个.

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
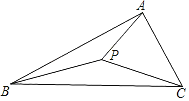
【题目】如图,在直角三角形△ABC内部有一动点P,∠BAC=90°,连接PA,PB,PC,若AC=6,AB=8,求PA+PB+PC的最小值_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
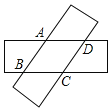
【题目】如图,两张等宽的纸条交叉重叠在一起,重叠的部分为四边形ABCD,若测得A,C之间的距离为12cm,点B,D之间的距离为16m,则线段AB的长为![]()
![]()
A. ![]() B. 10cmC. 20cmD. 12cm
B. 10cmC. 20cmD. 12cm
查看答案和解析>>
科目:初中数学 来源: 题型:
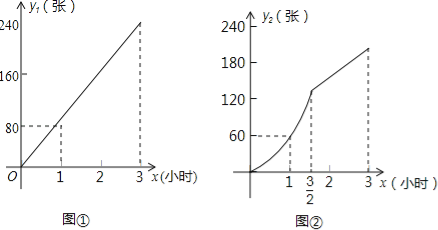
【题目】某市对火车站进行了大规模的改建,改建后的火车站除原有的普通售票窗口外,新增了自动打印车票的无人售票窗口.某日,从早8点开始到上午11点,每个普通售票窗口售出的车票数y1(张)与售票时间x(小时)的正比例函数关系满足图①中的图象,每个无人售票窗口售出的车票数y2(张)与售票时间x(小时)的函数关系满足图②中的图象.
(1)图②中图象的前半段(含端点)是以原点为顶点的抛物线的一部分,根据图中所给数据确定抛物线的表达式为 ,其中自变量x的取值范围是 ;
(2)若当天共开放5个无人售票窗口,截至上午9点,两种窗口共售出的车票数不少于1450张,则至少需要开放多少个普通售票窗口?
(3)上午10点时,每个普通售票窗口与每个无人售票窗口售出的车票数恰好相同,试确定图②中图象的后半段一次函数的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
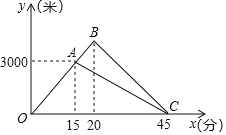
【题目】张琪和爸爸到曲江池遗址公园运动,两人同时从家出发,沿相同路线前行,途中爸爸有事返回,张琪继续前行5分钟后也原路返回,两人恰好同时到家张琪和爸爸在整个运动过程中离家的路点y1(米),y2(米)与运动时间x(分)之间的函数关系如图所示
(1)求爸爸返问时离家的路程y2(米)与运动时间x(分)之间的函数关系式;
(2)张琪开始返回时与爸爸相距多少米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com