
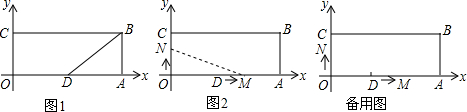
���� ��1�����ݵ�A�͵�C�������ȷ����OA��OC�ij����ɵ�D��OA���е����õ�D�������AD�ij���������������Ǻ����Ķ�����⼴�ɣ�
��2����ͼ1��ʾ������A��AE��ֱBD������ΪE���ɹ��ɶ������BD�ij���Ȼ���������ε������������AE�ij���Ȼ�����d��r�Ĺ�ϵ���жϳ�ֱ��DB��ԲA�Ĺ�ϵ���Ӷ���֪����ĸ�����
��3����ͼ2��3��4��ʾ���ɡ�MONΪֱ�������ο����t��ֵ��t��ȡֵ��Χ��
��� �⣺��1���ߵ�A�͵�C������ֱ�Ϊ��12��0���ͣ�0��4����
��OA=12��CO=4��
���ı���OABCΪ���Σ�
��OA=BC=12��OC=AB=4��
�ߵ�DΪOA���е㣬
���D��������6��0����AD=$\frac{1}{2}AO=\frac{1}{2}��12=6$��
��tan��BDA=$\frac{AB}{AD}=\frac{2}{3}$��
�ʴ�Ϊ����6��0����$\frac{2}{3}$��
��2����ͼ1��ʾ������A��AE��ֱBD������ΪE��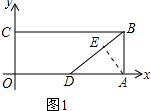
��Rt��ABD��DB=$\sqrt{A{D}^{2}+A{B}^{2}}=\sqrt{{6}^{2}+{4}^{2}}$=2$\sqrt{13}$��
�������ε������ʽ��֪��$\frac{1}{2}BD•AE=\frac{1}{2}AD•AB$����$\frac{1}{2}��2\sqrt{13}��AE=\frac{1}{2}��6��4$��
��ã�AE=$\frac{12\sqrt{13}}{13}$��
��AE��3����d��r��
��ֱ��BD���A���룮
��ֱ��BD���Aû�й����㣮
��3������ͼ2��ʾ��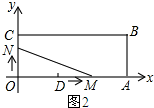
��OC=4��DA=6��
���N��O��C��Ҫ4s����M��D��A��Ҫ2s��
��0��t��2ʱ����N��OC�ϣ���M��DA�ϣ�
�൱0��t��2ʱ����AOMΪֱ�������Σ�
����ͼ3��ʾ����MN��OCʱ����MON��ֱ�������Σ�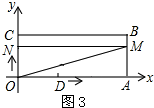
��MN��OC��
���MNO=90�㣮
���MNO=��NOA=��OAM��
���ı���OAMNΪ���Σ�
��ON=AM��
��t=3t-6��
��ã�t=3��
�൱t=3sʱ����AOMΪֱ�������Σ�
����ͼ4��ʾ������N���C�غ�ʱ����NOMΪֱ�������Σ�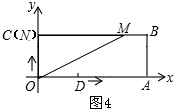
��ON=OC=4��
��3t=4��
��t=$\frac{4}{3}$
������������0��t��2ʱ��t=3ʱ��t=$\frac{4}{3}$ʱ����NOMΪֱ�������Σ�
���� ������Ҫ������Ǿ��ε����ʡ�������Ǻ����Ķ��塢ֱ�ߺ�Բ��λ�ù�ϵ�����ɶ�����Ӧ�ã��������⻭�����������ͼ���ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪��ֱ������ϵ�У�A��4��0����B��0��3�������߶�ABΪֱ�DZ��ڵ�һ������������Rt��ABC����BAC=90�㣮��P��x���ϵ�һ�����㣬��P��x��0����
��ͼ����֪��ֱ������ϵ�У�A��4��0����B��0��3�������߶�ABΪֱ�DZ��ڵ�һ������������Rt��ABC����BAC=90�㣮��P��x���ϵ�һ�����㣬��P��x��0�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com