
分析 (1)原式结合后,相加即可得到结果;
(2)原式结合后相加即可得到结果;
(3)原式利用绝对值的代数意义化简,计算即可得到结果;
(4)原式结合后,相加即可得到结果;
(5)原式利用减法法则变形,计算即可得到结果;
(6)原式去括号后计算即可得到结果.
解答 解:(1)原式=(-6.82-3.18)+(3.78-3.78)=-10;
(2)原式=-20+5=-15;
(3)原式=45+5-71-9=50-80=-40;
(4)原式=3$\frac{1}{4}$+5$\frac{3}{4}$-2$\frac{3}{5}$-8$\frac{2}{5}$=9-11=-2;
(5)原式=-3$\frac{1}{3}$+1$\frac{2}{3}$-$\frac{1}{2}$+4$\frac{3}{4}$=-$\frac{5}{3}$+$\frac{17}{4}$=$\frac{31}{12}$;
(6)原式=-1+3$\frac{3}{4}$-2.75=-1+1=0.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
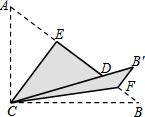 如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为( )
如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为( )| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com