
分析 根据二次根式有意义的条件可得2x-1≥0,1-2x≥0,再解可得x的值,进而可得y的值,然后再求$\frac{1}{2}xy$的平方根.
解答 解:由题意得:2x-1≥0,1-2x≥0,
解得:x=$\frac{1}{2}$,
则:y=$\frac{1}{4}$,
∵$\frac{1}{2}xy$=$\frac{1}{2}×\frac{1}{2}×\frac{1}{4}$=$\frac{1}{16}$,
∴$\frac{1}{2}xy$的平方根是±$\frac{1}{4}$,
故答案为:$±\frac{1}{4}$.
点评 此题主要考查了二次根式有意义的条件,关键是掌握被开方数必须是非负数.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:选择题
| A. | 5 | B. | $2\sqrt{7}$ | C. | 5或$\sqrt{7}$ | D. | 5或2$\sqrt{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
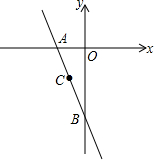 如图,直线y=kx+b经过点C(-1,-2),与x轴交于点A(-2,0),与y轴交于点B
如图,直线y=kx+b经过点C(-1,-2),与x轴交于点A(-2,0),与y轴交于点B查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{4}$=±2 | B. | ±$\sqrt{4}$=2 | C. | $\root{3}{-64}$=-4 | D. | $\sqrt{{{{(-2)}^2}}}$=-2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com