
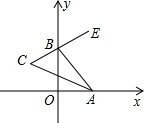
 如图,已知∠xOy=90°,点A、B分别在x轴、y轴上移动,BE是∠ABy的平分线,BE的反向延长线与∠OAB的平分线相交于点C,问:∠C的大小是否发生变化?如果保持不变,求出∠C的大小,如果随点A、B的移动发生变化,请求出∠C的变化范围.
如图,已知∠xOy=90°,点A、B分别在x轴、y轴上移动,BE是∠ABy的平分线,BE的反向延长线与∠OAB的平分线相交于点C,问:∠C的大小是否发生变化?如果保持不变,求出∠C的大小,如果随点A、B的移动发生变化,请求出∠C的变化范围. 分析 根据三角形的外角性质得出∠ABY=90°+∠OAB,角平分线的定义得出∠ABE=$\frac{1}{2}$∠ABY=$\frac{1}{2}$(90°+∠OAB),进一步代换求解.
解答 解:∠C的大小保持不变.
理由:∵∠ABY=90°+∠OAB,AC平分∠OAB,BE平分∠ABY,
∴∠ABE=$\frac{1}{2}$∠ABY=$\frac{1}{2}$(90°+∠OAB)=45°+$\frac{1}{2}$∠OAB,
即∠ABE=45°+∠CAB,
又∵∠ABE=∠C+∠CAB,
∴∠C=45°,
故∠ACB的大小不发生变化,且始终保持45°.
点评 本题考查的是三角形内角和定理:“三角形的内角和是180°”以及三角形的外角的性质.


 作业辅导系列答案
作业辅导系列答案科目:初中数学 来源: 题型:解答题
 写出下列各函数的表达式.指出它是什么函数,并确定函数的自变量的取值范围.
写出下列各函数的表达式.指出它是什么函数,并确定函数的自变量的取值范围.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.9x-190=190×0.152 | B. | 0.9x=190×0.152 | ||
| C. | 0.152x=190×0.9 | D. | 190-0.9x=190×0.152 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com